从傅里叶级数开始,后续过渡到傅里叶变换。
傅里叶级数(fourier series),几乎等同于周期性现象的学习。
傅里叶变换(fourier transform),可作为傅里叶级数的极限情况,是对非周期性现象的数学分析。
分析(analysis),分解一个信号(函数),把它拆分成一系列组成部分,并希望这些组成部分比复杂的原始信号(函数)简单。
合成(synthesis),把基本的组成部分重组成信号本身。
分析与合成总是成对出现,我们把复杂的信号分离成简单信号,然后进行我们需要的处理,最后再组合成原始信号。
傅里叶分析与合成是由线性运算完成的,线性运算包含有积分和序列。傅里叶分析经常被认为是线性分析的一部分。
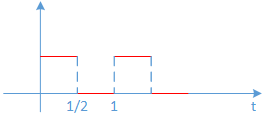
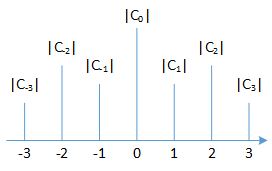
周期性现象有两种:
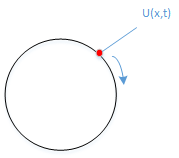
例:圆环上的热量分布
在这个例子里面认为温度不受时间影响,温度与圆环的位置有关。我们从圆环上的某点A测试圆环的温度,然后沿着顺时针方向一直测试,最终又会回到A点继续顺时针测试温度,这样我们就能得到呈现周期性的温度值。从上述测试我们可以得到初步结果:
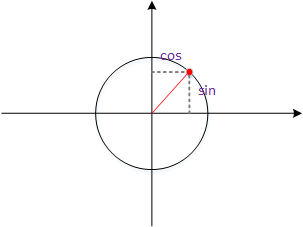
在时域上,用频率(frequency)表达。波长(λ \lambda λ 与 频率(ϑ \vartheta ϑ 属性。
波长,即某一时间点,一个完整波扰动的长度。
频率,1秒内出现波扰动的次数。
两者有以下关系:v v v v = λ ⋅ ϑ v=\lambda\cdot\vartheta v = λ ⋅ ϑ
由于数学上有sin \sin sin cos \cos cos cos ( T + 2 π ) = cos ( T ) \cos(T+2\pi)=\cos(T) cos ( T + 2 π ) = cos ( T ) sin \sin sin cos \cos cos sin \sin sin cos \cos cos
如何用像sin \sin sin cos \cos cos
并不是所有现象都是周期性的,而且即使是周期性的现象(时间周期性),最终都会终结。而sin \sin sin cos \cos cos
我们可以把它无限复制,这样就成了一个周期信号,然后研究我们感兴趣的部分(单一周期内的信号)。由于有了信号周期化这种做法,我们的傅里叶研究将相当广泛。
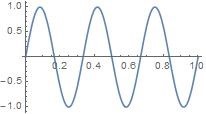
为了方便我们后面的学习,在此设定周期为1(归一化),后面的学习会遵循该设定,即f ( t + 1 ) = f ( t ) f(t+1) = f(t) f ( t + 1 ) = f ( t ) sin ( 2 π t ) \sin(2\pi t) sin ( 2 π t ) cos ( 2 π t ) \cos(2\pi t) cos ( 2 π t )
首先引出结论,周期为1的信号,可以由sin ( 2 π t ) \sin(2\pi t) sin ( 2 π t ) cos ( 2 π t ) \cos(2\pi t) cos ( 2 π t )
举个例子sin ( 2 π t ) \sin(2\pi t) sin ( 2 π t ) sin ( 4 π t ) \sin(4\pi t) sin ( 4 π t ) sin ( 6 π t ) \sin(6 \pi t) sin ( 6 π t )
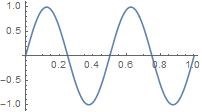
sin ( 2 π t ) \sin(2\pi t) sin ( 2 π t ) sin ( 4 π t ) \sin(4\pi t) sin ( 4 π t ) sin ( 6 π t ) \sin(6\pi t) sin ( 6 π t ) sin ( 2 π t ) + sin ( 4 π t ) + sin ( 6 π t ) \sin(2\pi t)+\sin(4\pi t)+\sin(6\pi t) sin ( 2 π t ) + sin ( 4 π t ) + sin ( 6 π t )
这个复杂的图形的周期还是1,它是由周期为1,频率不同的sin函数组成的。sin \sin sin
∑ k = 1 n A k sin ( 2 π k t + φ k ) \displaystyle{\sum^n_{k=1}}A_k \sin(2\pi kt+\varphi_k)
k = 1 ∑ n A k sin ( 2 π k t + φ k )
注:k = 1 k=1 k = 1 k > 1 k>1 k > 1
对sin \sin sin
sin ( 2 π k t + φ k ) = sin ( 2 π k t ) cos φ k + cos ( 2 π k t ) sin φ k \sin(2\pi kt + \varphi_k)=\sin(2\pi kt)\cos\varphi_k+\cos(2\pi kt)\sin\varphi_k
sin ( 2 π k t + φ k ) = sin ( 2 π k t ) cos φ k + cos ( 2 π k t ) sin φ k
因此有
∑ k = 1 n A k sin ( 2 π k t + φ k ) = ∑ k = 1 n A k sin ( 2 π k t ) cos φ k + cos ( 2 π k t ) sin φ k = ∑ k = 1 n ( a k cos ( 2 π k t ) + b k sin ( 2 π k t ) ) \begin{aligned}
&\quad \sum^n_{k=1}A_k\sin(2\pi kt + \varphi_k)\\
&=\sum^n_{k=1}A_k\sin(2\pi kt)\cos\varphi_k+\cos(2\pi kt)\sin\varphi_k\\
&=\sum^n_{k=1}(a_k\cos(2\pi kt)+b_k\sin(2\pi kt))
\end{aligned}
k = 1 ∑ n A k sin ( 2 π k t + φ k ) = k = 1 ∑ n A k sin ( 2 π k t ) cos φ k + cos ( 2 π k t ) sin φ k = k = 1 ∑ n ( a k cos ( 2 π k t ) + b k sin ( 2 π k t ) )
a k , b k a_k,b_k a k , b k φ k \varphi_k φ k A k A_k A k
a 0 2 + ∑ k = 1 n ( a k cos ( 2 π k t ) + b k sin ( 2 π k t ) ) \frac{a_0}{2}+\displaystyle{\sum^n_{k=1}}(a_k\cos(2\pi kt)+b_k\sin(2\pi kt))
2 a 0 + k = 1 ∑ n ( a k cos ( 2 π k t ) + b k sin ( 2 π k t ) )
该常量a 0 2 \frac{a_0}{2} 2 a 0
上面的式子还可以推导成复指数的方式
e 2 π i k t = cos ( 2 π k t ) + i sin ( 2 π k t ) , i = − 1 e^{2\pi ikt} = \cos(2\pi kt)+i\sin(2\pi kt), i=\sqrt{-1}
e 2 π i k t = cos ( 2 π k t ) + i sin ( 2 π k t ) , i = − 1
cos ( 2 π k t ) = e 2 π i k t + e − 2 π i k t 2 \cos(2\pi kt) = \frac{e^{2\pi ikt} + e^{-2\pi ikt}}{2}
cos ( 2 π k t ) = 2 e 2 π i k t + e − 2 π i k t
sin ( 2 π k t ) = e 2 π i k t − e − 2 π i k t 2 i \sin(2\pi kt) = \frac{e^{2\pi ikt} - e^{-2\pi ikt}}{2i}
sin ( 2 π k t ) = 2 i e 2 π i k t − e − 2 π i k t
通过欧拉公式对上述式子进行展开,得
a k cos ( 2 π k t ) + b k sin ( 2 π k t ) = a k e 2 π i k t + a k e − 2 π i k t 2 + b k e 2 π i k t − b k e − 2 π i k t 2 i = a k e 2 π i k t + a k e − 2 π i k t 2 + − b k i e 2 π i k t + b k i e − 2 π i k t 2 = a k − b k i 2 e 2 π i k t + a k + b k i 2 e − 2 π i k t \begin{aligned}
&\quad a_k\cos(2\pi kt)+b_k\sin(2\pi kt)\\
&= \frac{a_ke^{2\pi ikt}+a_ke^{-2\pi ikt}}{2}+\frac{b_ke^{2\pi ikt}-b_ke^{-2\pi ikt}}{2i}\\
&= \frac{a_ke^{2\pi ikt}+a_ke^{-2\pi ikt}}{2}+\frac{-b_kie^{2\pi ikt}+b_kie^{-2\pi ikt}}{2}\\
&= \frac{a_k-b_ki}{2}e^{2\pi ikt}+\frac{a_k+b_ki}{2}e^{-2\pi ikt}
\end{aligned}
a k cos ( 2 π k t ) + b k sin ( 2 π k t ) = 2 a k e 2 π i k t + a k e − 2 π i k t + 2 i b k e 2 π i k t − b k e − 2 π i k t = 2 a k e 2 π i k t + a k e − 2 π i k t + 2 − b k i e 2 π i k t + b k i e − 2 π i k t = 2 a k − b k i e 2 π i k t + 2 a k + b k i e − 2 π i k t
分成a k − b k i 2 e 2 π i k t \frac{a_k-b_ki}{2}e^{2\pi ikt} 2 a k − b k i e 2 π i k t a k + b k i 2 e − 2 π i k t \frac{a_k+b_ki}{2}e^{-2\pi ikt} 2 a k + b k i e − 2 π i k t k k k k k k k k k
a k cos ( 2 π k t ) + b k sin ( 2 π k t ) = a k − b k i 2 e 2 π i k t + a k + b k i 2 e − 2 π i k t ⏟ k > 0 = a k − b k i 2 e 2 π i k t ⏟ k > 0 + a − k + b − k i 2 e 2 π i k t ⏟ k < 0 \begin{aligned}
a_k\cos(2\pi kt)+b_k\sin(2\pi kt)
&= \underbrace{\frac{a_k-b_ki}{2}e^{2\pi ikt}+\frac{a_k+b_ki}{2}e^{-2\pi ikt}}_{k>0}\\
&= \underbrace{\frac{a_k-b_ki}{2}e^{2\pi ikt}}_{k>0}+\underbrace{\frac{a_{-k}+b_{-k}i}{2}e^{2\pi ikt}}_{k<0}
\end{aligned}
a k cos ( 2 π k t ) + b k sin ( 2 π k t ) = k > 0 2 a k − b k i e 2 π i k t + 2 a k + b k i e − 2 π i k t = k > 0 2 a k − b k i e 2 π i k t + k < 0 2 a − k + b − k i e 2 π i k t
把a k − b k i 2 \frac{a_k-b_ki}{2} 2 a k − b k i a − k + b − k i 2 \frac{a_{-k}+b_{-k}i}{2} 2 a − k + b − k i C k C_k C k
C k = { a k − b k i 2 , k > 0 a − k + b − k i 2 , k < 0 C_k=
\begin{cases}
&\frac{a_k-b_ki}{2} \text{ , } k>0 \\
&\frac{a_{-k}+b_{-k}i}{2} \text{ , } k<0
\end{cases}
C k = { 2 a k − b k i , k > 0 2 a − k + b − k i , k < 0
即C k C_k C k C − k = C k ˉ C_{-k}=\bar{C_k} C − k = C k ˉ
∑ k = 1 n ( a k cos ( 2 π k t ) + b k sin ( 2 π k t ) ) = ∑ k = − n n C k e 2 π i k t \begin{aligned}
&\quad \sum^n_{k=1}(a_k\cos(2\pi kt)+b_k\sin(2\pi kt))\\
&=\sum^n_{k=-n}C_ke^{2\pi ikt}
\end{aligned}
k = 1 ∑ n ( a k cos ( 2 π k t ) + b k sin ( 2 π k t ) ) = k = − n ∑ n C k e 2 π i k t
上述推导引出一个结论:对于一个真实的信号(值为实数),当它转换为上述复数形式时,它的系数对称存在,即有k k k − k -k − k C k C_k C k C − k C_{-k} C − k
我们已经从sin \sin sin
f ( t ) = ∑ k = − n n C k e 2 π i k t f(t)=\displaystyle{\sum^n_{k=-n}}C_ke^{2\pi ikt}
f ( t ) = k = − n ∑ n C k e 2 π i k t
取出该多项式其中的一项 C m e 2 π i m t , − n ⩽ m ⩽ n C_me^{2\pi imt},-n \leqslant m \leqslant n C m e 2 π i m t , − n ⩽ m ⩽ n C m e 2 π i m t = f ( t ) − ∑ k ≠ m n C k e 2 π i k t C_me^{2\pi imt} = f(t)-\displaystyle{\sum^n_{k\neq m}}C_k e^{2\pi ikt} C m e 2 π i m t = f ( t ) − k = m ∑ n C k e 2 π i k t e − 2 π i m t e^{-2\pi imt} e − 2 π i m t
C m = e − 2 π i m t f ( t ) − ∑ k ≠ m n C k e − 2 π i m t e 2 π i k t = e − 2 π i m t f ( t ) − ∑ k ≠ m n C k e 2 π i ( k − m ) t \begin{aligned}
& C_m = e^{-2\pi imt}f(t)-\sum^n_{k\neq m}C_k e^{-2\pi imt}e^{2\pi ikt}\\
&\quad \ = e^{-2\pi imt}f(t)-\sum^n_{k\neq m}C_k e^{2\pi i(k-m)t}
\end{aligned}
C m = e − 2 π i m t f ( t ) − k = m ∑ n C k e − 2 π i m t e 2 π i k t = e − 2 π i m t f ( t ) − k = m ∑ n C k e 2 π i ( k − m ) t
对等号两边同时积分∫ 0 1 C m d t = C m \displaystyle{\int_{0}^{1}}C_mdt=C_m ∫ 0 1 C m d t = C m
∫ 0 1 ( e − 2 π i m t f ( t ) − ∑ k ≠ m n C k e 2 π i ( k − m ) t ) d t = ∫ 0 1 e − 2 π i m t f ( t ) d t − ∑ k ≠ m n C k ∫ 0 1 e 2 π i ( k − m ) t d t = ∫ 0 1 e − 2 π i m t f ( t ) d t − ∑ k ≠ m n C k 1 2 π i ( k − m ) e 2 π i ( k − m ) t ∣ 0 1 = ∫ 0 1 e − 2 π i m t f ( t ) d t − ∑ k ≠ m n C k 1 2 π i ( k − m ) ( e 2 π ( k − m ) t − e 0 ) = ∫ 0 1 e − 2 π i m t f ( t ) d t − ∑ k ≠ m n C k 1 2 π i ( k − m ) ( cos 2 π ( k − m ) + i sin 2 π ( k − m ) − 1 ) s p r e a d w i t h E u l e r F o r m u l a r = ∫ 0 1 e − 2 π i m t f ( t ) d t − ∑ k ≠ m n C k 1 2 π i ( k − m ) ( 1 + 0 − 1 ) k a n d m i s i n t e r g e r = ∫ 0 1 e − 2 π i m t f ( t ) d t \begin{aligned}
&\quad \int_{0}^{1}(e^{-2\pi imt}f(t)-\sum^n_{k\neq m}C_k e^{2\pi i(k-m)t})dt \\
&= \int_{0}^{1}e^{-2\pi imt}f(t)dt - \sum^n_{k\neq m}C_k\int_{0}^{1} e^{2\pi i(k-m)t}dt \\
&= \int_{0}^{1}e^{-2\pi imt}f(t)dt - \sum^n_{k\neq m}C_k\left.\frac{1}{2\pi i(k-m)}e^{2\pi i(k-m)t}\right|^1_0 \\
&= \int_{0}^{1}e^{-2\pi imt}f(t)dt - \sum^n_{k\neq m}C_k\frac{1}{2\pi i(k-m)}(e^{2\pi (k-m)t}-e^0) \\
&= \int_{0}^{1}e^{-2\pi imt}f(t)dt - \sum^n_{k\neq m}C_k\frac{1}{2\pi i(k-m)}(\cos2\pi(k-m)+i\sin2\pi(k-m) - 1) \quad spread \ with \ Euler \ Formular \\
&= \int_{0}^{1}e^{-2\pi imt}f(t)dt - \sum^n_{k\neq m}C_k\frac{1}{2\pi i(k-m)}(1+0-1) \quad k \ and \ m \ is \ interger \\
&= \int_{0}^{1}e^{-2\pi imt}f(t)dt
\end{aligned}
∫ 0 1 ( e − 2 π i m t f ( t ) − k = m ∑ n C k e 2 π i ( k − m ) t ) d t = ∫ 0 1 e − 2 π i m t f ( t ) d t − k = m ∑ n C k ∫ 0 1 e 2 π i ( k − m ) t d t = ∫ 0 1 e − 2 π i m t f ( t ) d t − k = m ∑ n C k 2 π i ( k − m ) 1 e 2 π i ( k − m ) t ∣ ∣ ∣ ∣ 0 1 = ∫ 0 1 e − 2 π i m t f ( t ) d t − k = m ∑ n C k 2 π i ( k − m ) 1 ( e 2 π ( k − m ) t − e 0 ) = ∫ 0 1 e − 2 π i m t f ( t ) d t − k = m ∑ n C k 2 π i ( k − m ) 1 ( cos 2 π ( k − m ) + i sin 2 π ( k − m ) − 1 ) s p r e a d w i t h E u l e r F o r m u l a r = ∫ 0 1 e − 2 π i m t f ( t ) d t − k = m ∑ n C k 2 π i ( k − m ) 1 ( 1 + 0 − 1 ) k a n d m i s i n t e r g e r = ∫ 0 1 e − 2 π i m t f ( t ) d t
即,
C m = ∫ 0 1 e − 2 π i m t f ( t ) d t C_m = \displaystyle{\int_{0}^{1}}e^{-2\pi imt}f(t)dt
C m = ∫ 0 1 e − 2 π i m t f ( t ) d t
上节课,我们假设了一般周期函数可以用sin \sin sin
f ( t ) = ∑ k = − n n C k e 2 π i k t f(t)=\displaystyle{\sum_{k=-n}^n}C_ke^{2\pi ikt}
f ( t ) = k = − n ∑ n C k e 2 π i k t
然后,我们又推导出了C k C_k C k
C m = ∫ 0 1 e − 2 π i m t f ( t ) d t C_m=\displaystyle{\int_0^1}e^{-2\pi imt}f(t)dt
C m = ∫ 0 1 e − 2 π i m t f ( t ) d t
现在,我们为C m C_m C m f ^ ( k ) \hat{f}(k) f ^ ( k )
f ( t ) = ∑ k = − n n f ^ ( k ) e 2 π i k t f(t) = \displaystyle{\sum_{k=-n}^n}\hat{f}(k)e^{2\pi ikt}
f ( t ) = k = − n ∑ n f ^ ( k ) e 2 π i k t
f ^ ( k ) = ∫ 0 1 e − 2 π i k t f ( t ) d t \hat{f}(k) = \displaystyle{\int_0^1}e^{-2\pi ikt}f(t)dt
f ^ ( k ) = ∫ 0 1 e − 2 π i k t f ( t ) d t
现在回到通用性这个问题,那么f ( t ) = ∑ k = − n n f ^ ( k ) e 2 π i k t f(t) = \displaystyle{\sum_{k=-n}^n}\hat{f}(k)e^{2\pi ikt} f ( t ) = k = − n ∑ n f ^ ( k ) e 2 π i k t
我们可以简单地得到该函数的傅里叶系数,
f ^ ( k ) = ∫ 0 1 2 e − 2 π i k t d t \hat{f}(k) = \displaystyle{\int_0^{\frac{1}{2}}}e^{-2\pi ikt}dt
f ^ ( k ) = ∫ 0 2 1 e − 2 π i k t d t
其中,k k k e − 2 π i k t e^{-2\pi ikt} e − 2 π i k t 0 0 0 1 2 \frac{1}{2} 2 1
f ( t ) = ∑ k = − n n f ^ ( k ) e 2 π i k t f(t) = \displaystyle{\sum_{k=-n}^n} \hat{f}(k)e^{2\pi ikt}
f ( t ) = k = − n ∑ n f ^ ( k ) e 2 π i k t
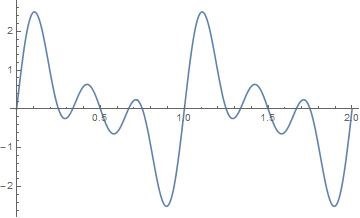
答案是否定的! 还记得公式最初是从
f ( t ) = ∑ k = 1 n A k s i n ( 2 π k t + φ k ) f(t)=\displaystyle{\sum_{k=1}^n}A_ksin(2\pi kt+\varphi_k)
f ( t ) = k = 1 ∑ n A k s i n ( 2 π k t + φ k )
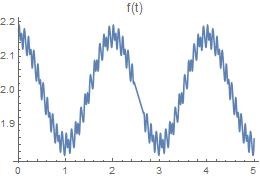
推导的么,对于上述信号的等式, 等号的右边是三角函数的组合,因此无限可微,而左边,如上图,是不连续的,因此不是无限可微的,因此式子两边不能画上等号!
从几何图形上看,对于sin \sin sin
f ( t ) = ∑ k = − ∞ ∞ f ^ ( k ) e 2 π i k t f(t) = \displaystyle{\sum_{k=-\infty}^{\infty}} \hat{f}(k)e^{2\pi ikt}
f ( t ) = k = − ∞ ∑ ∞ f ^ ( k ) e 2 π i k t
在引入了∞ \infty ∞
如果信号是平滑连续的(连续可微),在所有的t t t f ( t ) f(t) f ( t )
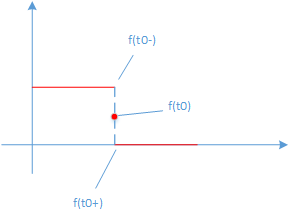
如果信号是有跳变的,在跳变点将收敛于跳变点前、后的平均值。如下例子:
设t 0 t_0 t 0 ∑ k = − ∞ ∞ f ^ ( k ) e 2 π i k t 0 \displaystyle{\sum_{k=-\infty}^{\infty}}\hat{f}(k)e^{2\pi ikt_0} k = − ∞ ∑ ∞ f ^ ( k ) e 2 π i k t 0 f ( t 0 + ) + f ( t 0 − ) 2 \frac{f(t_0^+)+f(t_0^-)}{2} 2 f ( t 0 + ) + f ( t 0 − ) 均方收敛(convergence in the mean)。
∫ 0 1 ∣ f ( t ) ∣ 2 d t < ∞ \displaystyle{\int_0^1}\left| f(t) \right|^2dt<\infty
∫ 0 1 ∣ f ( t ) ∣ 2 d t < ∞
上面的式子可以被理解为能量是有限的,这是一个合理的物理假设。均方收敛的分析公式如下:
∫ 0 1 ∣ ∑ k = − n n f ^ ( t ) e 2 π i k t − f ( t ) ∣ 2 d t \displaystyle{\int_0^1\left| \sum^{n}_{k=-n}\hat{f}(t)e^{2\pi ikt}-f(t) \right|^2dt}
∫ 0 1 ∣ ∣ ∣ ∣ ∣ k = − n ∑ n f ^ ( t ) e 2 π i k t − f ( t ) ∣ ∣ ∣ ∣ ∣ 2 d t
当n → ∞ n \to \infty n → ∞ → 0 \to 0 → 0 ∑ k = − ∞ ∞ f ^ ( k ) e 2 π i k t \displaystyle{\sum_{k=-\infty}^{\infty}}\hat{f}(k)e^{2\pi ikt} k = − ∞ ∑ ∞ f ^ ( k ) e 2 π i k t f ( t ) f(t) f ( t )
在上节课最后,引出了均方收敛,
∫ 0 1 ∣ ∑ k = − n n f ^ ( k ) e 2 π i k t − f ( t ) ∣ 2 d t → 0 if n → ∞ \displaystyle{\int_0^1\left| \sum_{k=-n}^{n}\hat{f}(k)e^{2\pi ikt}-f(t)\right|^2 dt} \to 0 \ \text{if} \ n \to \infty
∫ 0 1 ∣ ∣ ∣ ∣ ∣ k = − n ∑ n f ^ ( k ) e 2 π i k t − f ( t ) ∣ ∣ ∣ ∣ ∣ 2 d t → 0 if n → ∞
均方收敛的这种分析方法需要f(t)满足一个条件:f ( t ) f(t) f ( t ) [ 0 , 1 ] [0,1] [ 0 , 1 ] ∫ 0 1 ∣ f ( t ) ∣ 2 d t < ∞ \displaystyle{\int_0^1\left|f(t)\right|^2dt<\infty} ∫ 0 1 ∣ f ( t ) ∣ 2 d t < ∞ f ∈ L 2 ( [ 0 , 1 ] ) f\in L^2([0,1]) f ∈ L 2 ( [ 0 , 1 ] )
还记得我们在推导傅里叶式子的时候用了一个积分:
∫ 0 1 e 2 π i k t e − 2 π i m t d t = ∫ 0 1 e 2 π i ( k − m ) t d t = 0 , k ≠ m \displaystyle{\int_0^1e^{2\pi ikt}e^{-2\pi imt}dt = \int_0^1e^{2\pi i(k-m)t}dt = 0, \quad k\neq m}
∫ 0 1 e 2 π i k t e − 2 π i m t d t = ∫ 0 1 e 2 π i ( k − m ) t d t = 0 , k = m
这个简单的式子,将把“几何”引入到平方可积函数中L 2 ( [ 0 , 1 ] ) L^2([0,1]) L 2 ( [ 0 , 1 ] ) f , g ∈ L 2 ( [ 0 , 1 ] ) f,g\in L^2([0,1]) f , g ∈ L 2 ( [ 0 , 1 ] ) f , g f,g f , g
( f , g ) = ∫ 0 1 f ( t ) g ˉ ( t ) d t (f,g) = \displaystyle{\int_0^1f(t)\bar{g}(t)dt}
( f , g ) = ∫ 0 1 f ( t ) g ˉ ( t ) d t
当( f , g ) = 0 (f,g)=0 ( f , g ) = 0 f f f g g g
类比到向量的模,也就是求向量的平方。
( f , f ) = ∥ f ∥ 2 = ∫ 0 1 ∣ f ( t ) ∣ 2 d t \displaystyle{(f,f)=\left \| f \right \|^2=\int_0^1\left| f(t) \right| ^2dt}
( f , f ) = ∥ f ∥ 2 = ∫ 0 1 ∣ f ( t ) ∣ 2 d t
∥ f + g ∥ 2 = ∥ f ∥ 2 + ∥ g ∥ 2 \displaystyle{\left \| f+g \right \|^2 = \left \| f \right \|^2 + \left \| g \right \|^2 }
∥ f + g ∥ 2 = ∥ f ∥ 2 + ∥ g ∥ 2
当且仅当( f , g ) = 0 (f,g)=0 ( f , g ) = 0
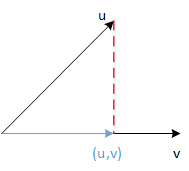
利用向量的内积来定义并计算投影(projections)。几何上的投影如下图:
如果v v v ( u , v ) (u,v) ( u , v ) u u u v v v 类比到傅里叶系数:
f ^ ( n ) = ∫ 0 1 f ( t ) e − 2 π i n t d t = ( f ( t ) , e 2 π i n t ) \displaystyle{\hat{f}(n)=\int_0^1f(t)e^{-2\pi int}dt = (f(t), e^{2\pi int})}
f ^ ( n ) = ∫ 0 1 f ( t ) e − 2 π i n t d t = ( f ( t ) , e 2 π i n t )
因此傅里叶系数f ^ ( n ) \hat{f}(n) f ^ ( n ) f ( t ) f(t) f ( t ) e 2 π i n t e^{2\pi int} e 2 π i n t
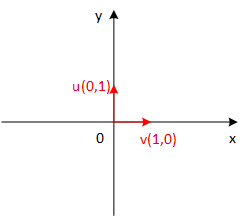
几何上的正交基如下图:
u = ( 0 , 1 ) , v = ( 1 , 0 ) u = (0,1), \ v = (1,0) u = ( 0 , 1 ) , v = ( 1 , 0 ) u , v u,v u , v ( u , u ) = u 2 = 1 , ( v , v ) = v 2 = 1 (u,u) = u^2 = 1, \ (v,v) = v^2 = 1 ( u , u ) = u 2 = 1 , ( v , v ) = v 2 = 1 ( u , v ) = 0 (u,v) = 0 ( u , v ) = 0
( e 2 π i m t , e 2 π i k t ) = { 1 m = k 0 m ≠ k (e^{2\pi imt}, e^{2\pi ikt}) = \left\{\begin{matrix}
1 & m = k \\
0 & m \neq k
\end{matrix}\right.
( e 2 π i m t , e 2 π i k t ) = { 1 0 m = k m = k
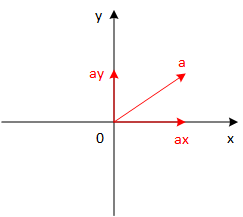
几何上,一个向量a a a
设x , y x,y x , y u , v u,v u , v a a a x , y x,y x , y a x = ( a , u ) u , a y = ( a , v ) v a_x = (a,u)u, \ a_y = (a,v)v a x = ( a , u ) u , a y = ( a , v ) v f ( t ) f(t) f ( t )
f ( t ) = ∑ k = − ∞ ∞ f ^ ( t ) e 2 π i k t = ∑ k = − ∞ ∞ ( f , e 2 π i k t ) e 2 π i k t \begin{aligned}
\displaystyle{f(t)}
&= \displaystyle{\sum_{k=-\infty}^{\infty}\hat{f}(t)e^{2\pi ikt} } \\
&= \displaystyle{\sum_{k=-\infty}^{\infty}(f, e^{2\pi ikt})e^{2\pi ikt} }
\end{aligned}
f ( t ) = k = − ∞ ∑ ∞ f ^ ( t ) e 2 π i k t = k = − ∞ ∑ ∞ ( f , e 2 π i k t ) e 2 π i k t
函数进行傅里叶变换后的每一项,都是函数在正交基e 2 π i k t e^{2\pi ikt} e 2 π i k t
几何向量有勾股定理: c 2 = a 2 + b 2 , ( a , b ) = 0 c^2 = a^2 + b^2, \ (a,b) = 0 c 2 = a 2 + b 2 , ( a , b ) = 0 类比到傅里叶变换有瑞利等式如下:
∫ 0 1 ∣ f ( t ) ∣ 2 d t = ∑ k = − ∞ ∞ ∣ f ^ ( k ) ∣ 2 \displaystyle{\int_0^1 \left | f(t) \right |^2dt = \sum_{k=-\infty}^{\infty} \left | \hat{f}(k) \right |^2 }
∫ 0 1 ∣ f ( t ) ∣ 2 d t = k = − ∞ ∑ ∞ ∣ ∣ ∣ f ^ ( k ) ∣ ∣ ∣ 2
傅里叶变换后的项互为正交项,正交项内积为0。
研究的问题如下:f ( x ) f(x) f ( x ) x x x 热环
x x x U ( x , t ) U(x,t) U ( x , t ) x x x t t t f ( x + 1 ) = f ( x ) f(x+1) = f(x) f ( x + 1 ) = f ( x ) U ( x + 1 , t ) = U ( x , t ) U(x+1,t) = U(x,t) U ( x + 1 , t ) = U ( x , t )
U ( x , t ) = ∑ k = − ∞ ∞ C k e 2 π i k x U(x,t) = \displaystyle{\sum_{k=-\infty}^{\infty}C_k e^{2\pi ikx} }
U ( x , t ) = k = − ∞ ∑ ∞ C k e 2 π i k x
另外还有时间变量t t t t t t C k C_k C k
U ( x , t ) = ∑ k = − ∞ ∞ C k ( t ) e 2 π i k x U(x,t) = \displaystyle{\sum_{k=-\infty}^{\infty}C_k(t)e^{2\pi ikx} }
U ( x , t ) = k = − ∞ ∑ ∞ C k ( t ) e 2 π i k x
现在我们的目的就变成了求傅里叶系数C k ( t ) C_k(t) C k ( t ) C k ( t ) C_k(t) C k ( t ) U t = a U x x U_t = aU_{xx} U t = a U x x U t U_t U t U U U t t t U x x U_{xx} U x x U U U x x x a = 1 2 a=\frac{1}{2} a = 2 1 U t = 1 2 U x x \color{blue}{U_t} = \color{red}{\frac{1}{2}U_{xx}} U t = 2 1 U x x U ( x , t ) = ∑ k = − ∞ ∞ C k ( t ) e 2 π i k x U(x,t) = \displaystyle{\sum_{k=-\infty}^{\infty}C_k(t)e^{2\pi ikx} } U ( x , t ) = k = − ∞ ∑ ∞ C k ( t ) e 2 π i k x
U t = ∑ k = − ∞ ∞ C k ′ ( t ) e 2 π i k x \color{blue}{U_t} = \displaystyle{\sum_{k=-\infty}^{\infty}\color{blue}{C_k'(t)}e^{2\pi ikx} }
U t = k = − ∞ ∑ ∞ C k ′ ( t ) e 2 π i k x
1 2 U x x = 1 2 ∑ k = − ∞ ∞ C k ( t ) ( 2 π i k ) 2 e 2 π i k x = 1 2 ∑ k = − ∞ ∞ C k ( t ) ( − 4 π 2 k 2 ) e 2 π i k x = ∑ k = − ∞ ∞ C k ( t ) ( − 2 π 2 k 2 ) e 2 π i k x \begin{aligned}
\color{red}{\frac{1}{2}U_{xx}}
&= \frac{1}{2} \displaystyle{\sum_{k=-\infty}^{\infty}C_k(t)(2\pi ik)^2 e^{2\pi ikx} } \\
&= \frac{1}{2} \displaystyle{\sum_{k=-\infty}^{\infty}C_k(t)(-4\pi^2k^2)e^{2\pi ikx} } \\
&= \displaystyle{\sum_{k=-\infty}^{\infty}\color{red}{C_k(t)(-2\pi^2k^2)}e^{2\pi ikx} }
\end{aligned}
2 1 U x x = 2 1 k = − ∞ ∑ ∞ C k ( t ) ( 2 π i k ) 2 e 2 π i k x = 2 1 k = − ∞ ∑ ∞ C k ( t ) ( − 4 π 2 k 2 ) e 2 π i k x = k = − ∞ ∑ ∞ C k ( t ) ( − 2 π 2 k 2 ) e 2 π i k x
两边对比得,C k ′ ( t ) = − 2 π 2 k 2 C k ( t ) for all k ∈ Z \color{blue}{C_k'(t)} = \color{red}{-2\pi^2k^2C_k(t)}\qquad \text{for all }k\in \mathbb{Z} C k ′ ( t ) = − 2 π 2 k 2 C k ( t ) for all k ∈ Z
C k ( t ) = C k ( 0 ) e − 2 π 2 k 2 t C_k(t) = C_k(0)e^{-2\pi^2k^2t}
C k ( t ) = C k ( 0 ) e − 2 π 2 k 2 t
上节课推导出热方程的傅里叶系数:C k ( t ) = C k ( 0 ) e − 2 π 2 k 2 t C_k(t) = C_k(0)e^{-2\pi ^2 k^2t} C k ( t ) = C k ( 0 ) e − 2 π 2 k 2 t C k ( 0 ) C_k(0) C k ( 0 )
U ( x , t ) = ∑ k = − ∞ ∞ C k ( t ) e 2 π i k x U(x,t) = \displaystyle{\sum_{k=-\infty}^{\infty}C_k(t)e^{2\pi ikx} }
U ( x , t ) = k = − ∞ ∑ ∞ C k ( t ) e 2 π i k x
当t = 0 t=0 t = 0
f ( x ) = U ( x , 0 ) = ∑ k = − ∞ ∞ C k ( 0 ) e 2 π i k x f(x) = U(x,0) = \displaystyle{\sum_{k=-\infty}^{\infty}C_k(0)e^{2\pi ikx} } f ( x ) = U ( x , 0 ) = k = − ∞ ∑ ∞ C k ( 0 ) e 2 π i k x
则,C k ( 0 ) C_k(0) C k ( 0 ) f ( x ) f(x) f ( x ) C k ( 0 ) = f ^ ( k ) C_k(0) = \hat{f}(k) C k ( 0 ) = f ^ ( k )
U ( x , t ) = ∑ k = − ∞ ∞ f ^ ( k ) e − 2 π 2 k 2 t e 2 π i k x U(x,t) = \displaystyle{\sum_{k=-\infty}^{\infty}\hat{f}(k)e^{-2\pi^2k^2t}e^{2\pi ikx} }
U ( x , t ) = k = − ∞ ∑ ∞ f ^ ( k ) e − 2 π 2 k 2 t e 2 π i k x
温度U U U t t t t → ∞ t \to \infty t → ∞ − 2 π 2 k 2 t → − ∞ -2\pi^2k^2t \to -\infty − 2 π 2 k 2 t → − ∞ e − 2 π 2 k 2 t → 0 e^{-2\pi^2k^2t} \to 0 e − 2 π 2 k 2 t → 0 U → 0 U \to 0 U → 0
我们可以对热方程中的f ^ ( k ) \hat{f}(k) f ^ ( k ) f ^ ( k ) = ∫ 0 1 e − 2 π i k y f ( y ) d y \hat{f}(k) = \displaystyle{\int_0^1 e^{-2\pi iky}f(y)dy} f ^ ( k ) = ∫ 0 1 e − 2 π i k y f ( y ) d y f ( x ) f(x) f ( x ) U ( x , t ) U(x,t) U ( x , t ) x x x f ( x ) f(x) f ( x ) f ( y ) f(y) f ( y ) f ^ ( k ) \hat{f}(k) f ^ ( k )
U ( x , t ) = ∑ k = − ∞ ∞ ( ∫ 0 1 e − 2 π i k y f ( y ) d y ) e − 2 π 2 k 2 t e 2 π i k x = ∫ 0 1 ( ∑ k = − ∞ ∞ e − 2 π i k y e 2 π i k x e − 2 π 2 k 2 t ) f ( y ) d y = ∫ 0 1 ( ∑ k = − ∞ ∞ e 2 π i k ( x − y ) e − 2 π 2 k 2 t ) f ( y ) d y \begin{aligned}
U(x,t) &=\displaystyle{\sum_{k=-\infty}^{\infty}(\int_0^1 e^{-2\pi iky}f(y)dy) e^{-2\pi^2k^2t}e^{2\pi ikx}} \\
&=\displaystyle{\int_0^1(\sum_{k=-\infty}^{\infty}e^{-2\pi iky}e^{2\pi ikx}e^{-2\pi^2k^2t})f(y)dy } \\
&=\displaystyle{\int_0^1(\sum_{k=-\infty}^{\infty}e^{2\pi ik(x-y)}e^{-2\pi^2k^2t})f(y)dy }
\end{aligned}
U ( x , t ) = k = − ∞ ∑ ∞ ( ∫ 0 1 e − 2 π i k y f ( y ) d y ) e − 2 π 2 k 2 t e 2 π i k x = ∫ 0 1 ( k = − ∞ ∑ ∞ e − 2 π i k y e 2 π i k x e − 2 π 2 k 2 t ) f ( y ) d y = ∫ 0 1 ( k = − ∞ ∑ ∞ e 2 π i k ( x − y ) e − 2 π 2 k 2 t ) f ( y ) d y
令g ( x , t ) = ∑ k = − ∞ ∞ e 2 π i k x e − 2 π 2 k 2 t g(x,t) = \displaystyle{\sum_{k=-\infty}^{\infty}e^{2\pi ikx}e^{-2\pi^2k^2t} } g ( x , t ) = k = − ∞ ∑ ∞ e 2 π i k x e − 2 π 2 k 2 t
U ( x , t ) = ∫ 0 1 g ( x − y , t ) f ( y ) d y U(x,t) = \displaystyle{\int_0^1g(x-y,t)f(y)dy }
U ( x , t ) = ∫ 0 1 g ( x − y , t ) f ( y ) d y
如上面的等式,热方程被转换成了卷积的表现形式
傅里叶级数到傅里叶变换是从周期现象到非周期现象的转变,我们可以将非周期函数看做是周期函数的一种特殊情况:周期趋于无穷。
C k = f ^ ( k ) = ∫ 0 1 e − 2 π i k t f ( t ) d t C_k = \displaystyle{\hat{f}(k) = \int_0^1e^{-2\pi ikt}f(t)dt }
C k = f ^ ( k ) = ∫ 0 1 e − 2 π i k t f ( t ) d t
f ( t ) = ∑ k = − ∞ ∞ f ^ ( k ) e 2 π i k t f(t) = \displaystyle{\sum_{k=-\infty}^{\infty}\hat{f}(k)e^{2\pi ikt} }
f ( t ) = k = − ∞ ∑ ∞ f ^ ( k ) e 2 π i k t
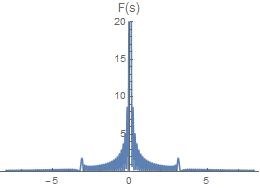
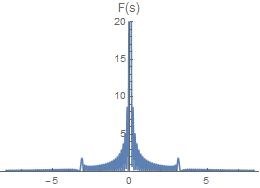
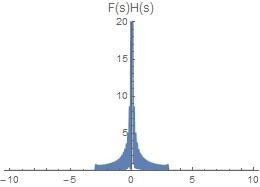
频谱图如下
由于周期为T T T 1 T \frac{1}{T} T 1 T → ∞ T \to \infty T → ∞ 1 T → 0 \frac{1}{T} \to 0 T 1 → 0
T → ∞ T \to \infty T → ∞ 但是是否仅仅让T → ∞ T \to \infty T → ∞ f ( t ) f(t) f ( t )
该函数的傅里叶系数求解过程如下:
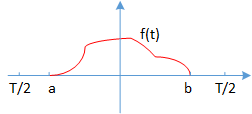
C k = f ^ ( k ) = 1 T ∫ − T 2 T 2 e − 2 π i k T t f ( t ) d t = 1 T ∫ a b e − 2 π i k T t f ( t ) d t ⩽ 1 T ∫ a b ∣ e − 2 π i k T t ∣ ∣ f ( t ) ∣ d t = 1 T ∫ a b M o d ( e − 2 π i k T t ) ∣ f ( t ) ∣ d t = 1 T ∫ a b M o d ( cos ( − 2 π k T t ) + i sin ( − 2 π k T t ) ) ∣ f ( t ) ∣ d t s p r e a d w i t h E u l a r F o r m u l a = 1 T ∫ a b cos 2 ( − 2 π k T t ) + sin 2 ( − 2 π k T t ) ∣ f ( t ) ∣ d t = 1 T ∫ a b 1 ∣ f ( t ) ∣ d t = 1 T ∫ a b ∣ f ( t ) ∣ d t = M T . \begin{aligned}
C_k = \displaystyle{\hat{f}(k) }
&= \displaystyle{\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}e^{-2\pi i\frac{k}{T}t}f(t)dt } \\
&= \displaystyle{\frac{1}{T}\int_a^b e^{-2\pi i\frac{k}{T}t}f(t)dt } \\
&\leqslant \displaystyle{\frac{1}{T}\int_a^b \left | e^{-2\pi i\frac{k}{T}t}\right | \left |f(t) \right |dt } \\
&= \displaystyle{\frac{1}{T}\int_a^b Mod(e^{-2\pi i\frac{k}{T}t}) \left |f(t) \right |dt } \\
&= \displaystyle{\frac{1}{T}\int_a^b Mod(\cos(-2\pi \frac{k}{T}t) + i\sin(-2\pi \frac{k}{T}t)) \left |f(t) \right |dt } \quad spread \ with \ Eular \ Formula \\
&= \displaystyle{\frac{1}{T}\int_a^b \sqrt{\cos^2(-2\pi \frac{k}{T}t) + \sin^2(-2\pi \frac{k}{T}t)} \left |f(t) \right |dt } \\
&= \displaystyle{\frac{1}{T}\int_a^b 1\left |f(t) \right |dt } \\
&= \displaystyle{\frac{1}{T}\int_a^b \left |f(t) \right |dt } \\
&= \frac{M}{T}
\end{aligned}.
C k = f ^ ( k ) = T 1 ∫ − 2 T 2 T e − 2 π i T k t f ( t ) d t = T 1 ∫ a b e − 2 π i T k t f ( t ) d t ⩽ T 1 ∫ a b ∣ ∣ ∣ e − 2 π i T k t ∣ ∣ ∣ ∣ f ( t ) ∣ d t = T 1 ∫ a b M o d ( e − 2 π i T k t ) ∣ f ( t ) ∣ d t = T 1 ∫ a b M o d ( cos ( − 2 π T k t ) + i sin ( − 2 π T k t ) ) ∣ f ( t ) ∣ d t s p r e a d w i t h E u l a r F o r m u l a = T 1 ∫ a b cos 2 ( − 2 π T k t ) + sin 2 ( − 2 π T k t ) ∣ f ( t ) ∣ d t = T 1 ∫ a b 1 ∣ f ( t ) ∣ d t = T 1 ∫ a b ∣ f ( t ) ∣ d t = T M .
即对于所有C k C_k C k C k ⩽ M T C_k \leqslant \frac{M}{T} C k ⩽ T M M M M T → ∞ T \to \infty T → ∞ C k → 0 C_k \to 0 C k → 0
上节课讲到,在对非周期函数进行傅里叶分析时,有
C k = 1 T ∫ − T 2 T 2 f ( t ) e − 2 π i k T t d t C_k = \displaystyle{\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f(t)e^{-2\pi i\frac{k}{T}t}dt }
C k = T 1 ∫ − 2 T 2 T f ( t ) e − 2 π i T k t d t
f ( t ) = ∑ k = − ∞ ∞ C k e 2 π i k T t f(t) = \displaystyle{\sum_{k=-\infty}^{\infty}C_ke^{2\pi i\frac{k}{T}t} }
f ( t ) = k = − ∞ ∑ ∞ C k e 2 π i T k t
我们希望仅让T → ∞ T\to \infty T → ∞ C k C_k C k C k ⩽ M T C_k \leqslant \frac{M}{T} C k ⩽ T M T → ∞ , C k → 0 T \to \infty \ ,C_k \to 0 T → ∞ , C k → 0 C k C_k C k T T T T T T C k C_k C k
F \mathcal{F} F 令
F f ( k T ) = C k × T = ∫ − T 2 T 2 e − 2 π i k T t f ( t ) d t \displaystyle{\mathcal{F} f(\frac{k}{T}) =C_k \times T = \int_{-\frac{T}{2}}^{\frac{T}{2}}e^{-2\pi i \frac{k}{T}t}f(t)dt }
F f ( T k ) = C k × T = ∫ − 2 T 2 T e − 2 π i T k t f ( t ) d t
即有,
f ( t ) = ∑ k = − ∞ ∞ F f ( k T ) e 2 π i k T t 1 T f(t) = \displaystyle{\sum_{k=-\infty}^{\infty}\mathcal{F} f(\frac{k}{T})e^{2\pi i\frac{k}{T}t} \frac{1}{T} }
f ( t ) = k = − ∞ ∑ ∞ F f ( T k ) e 2 π i T k t T 1
现在令T → ∞ T \to \infty T → ∞ k T \frac{k}{T} T k ( k = − ∞ T → ∞ , k = + ∞ T → ∞ ) (\frac{k=-\infty}{T\to \infty},\frac{k=+\infty}{T\to \infty}) ( T → ∞ k = − ∞ , T → ∞ k = + ∞ ) ( − ∞ , + ∞ ) (-\infty, +\infty) ( − ∞ , + ∞ ) 1 T → 0 \frac{1}{T} \to 0 T 1 → 0 s s s k T \frac{k}{T} T k s = k T , − ∞ < s < ∞ s = \frac{k}{T} \ , -\infty < s < \infty s = T k , − ∞ < s < ∞
F f ( s ) = ∫ − ∞ ∞ e − 2 π i s t f ( t ) d t \mathcal{F} f(s) = \displaystyle{\int_{-\infty}^{\infty}e^{-2\pi ist}f(t)dt }
F f ( s ) = ∫ − ∞ ∞ e − 2 π i s t f ( t ) d t
由于k T \frac{k}{T} T k s s s 1 T \frac{1}{T} T 1 △ s \bigtriangleup s △ s d s ds d s
f ( t ) = ∫ − ∞ ∞ F f ( s ) e 2 π i s t d s f(t) = \displaystyle{\int_{-\infty}^{\infty}\mathcal{F} f(s)e^{2\pi ist}ds }
f ( t ) = ∫ − ∞ ∞ F f ( s ) e 2 π i s t d s
如果f ( t ) f(t) f ( t ) − ∞ < T < ∞ -\infty < T < \infty − ∞ < T < ∞
F f ( s ) = ∫ − ∞ ∞ e − 2 π i s t f ( t ) d t \mathcal{F} f(s) = \displaystyle{\int_{-\infty}^{\infty} e^{-2\pi ist}f(t)dt }
F f ( s ) = ∫ − ∞ ∞ e − 2 π i s t f ( t ) d t
傅里叶逆变换:
f ( t ) = ∫ − ∞ ∞ e 2 π i s t F f ( s ) d s f(t) = \displaystyle{\int_{-\infty}^{\infty}e^{2\pi ist} \mathcal{F} f(s)ds }
f ( t ) = ∫ − ∞ ∞ e 2 π i s t F f ( s ) d s
也可以写作如下形式:
F f ( s ) = ∫ − ∞ ∞ e − 2 π i s t f ( t ) d t \mathcal{F} f(s) = \displaystyle{\int_{-\infty}^{\infty} e^{-2\pi ist}f(t)dt }
F f ( s ) = ∫ − ∞ ∞ e − 2 π i s t f ( t ) d t
F − 1 g ( t ) = ∫ − ∞ ∞ e 2 π i s t g ( s ) d s \mathcal{F}^{-1}g(t) = \displaystyle{\int_{-\infty}^{\infty}e^{2\pi ist}g(s)ds }
F − 1 g ( t ) = ∫ − ∞ ∞ e 2 π i s t g ( s ) d s
符号F \mathcal{F} F F − 1 \mathcal{F}^{-1} F − 1
F f ( 0 ) = ∫ − ∞ ∞ e − 2 π i 0 t f ( t ) d t = ∫ − ∞ ∞ f ( t ) d t \mathcal{F} f(0) = \displaystyle{\int_{-\infty}^{\infty} e^{-2\pi i0t}f(t)dt = \int_{-\infty}^{\infty}f(t)dt }
F f ( 0 ) = ∫ − ∞ ∞ e − 2 π i 0 t f ( t ) d t = ∫ − ∞ ∞ f ( t ) d t
F − 1 g ( 0 ) = ∫ − ∞ ∞ e 2 π i s 0 g ( s ) d s = ∫ − ∞ ∞ g ( s ) d s \mathcal{F}^{-1}g(0) = \displaystyle{\int_{-\infty}^{\infty}e^{2\pi is0} g(s)ds = \int_{-\infty}^{\infty}g(s)ds }
F − 1 g ( 0 ) = ∫ − ∞ ∞ e 2 π i s 0 g ( s ) d s = ∫ − ∞ ∞ g ( s ) d s
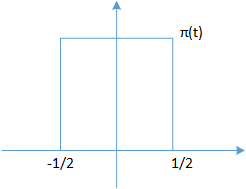
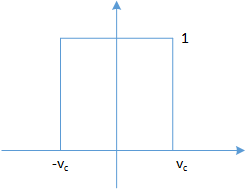
π ( t ) = { 1 ∣ t ∣ < 1 2 0 ∣ t ∣ ⩾ 1 2 \pi (t) =
\left\{\begin{matrix}
1 & \left| t \right| < \frac{1}{2}\\
0 & \left| t \right| \geqslant \frac{1}{2}
\end{matrix}\right. π ( t ) = { 1 0 ∣ t ∣ < 2 1 ∣ t ∣ ⩾ 2 1
傅里叶变换如下:
F π ( s ) = ∫ − ∞ ∞ e − 2 π i s t π ( t ) d t = ∫ − 1 2 1 2 e − 2 π i s t d t = − 1 2 π i s e − 2 π i s t ∣ 1 2 1 2 = − 1 2 π i s e − 2 π i s 1 2 − ( − 1 2 π i s e − 2 π i s ( − 1 2 ) ) = − 1 2 π i s e − π i s + 1 2 π i s e π i s = 1 π s ( e π i s − e − π i s 2 i ) = 1 π s ( cos ( π s ) + i sin ( π s ) − cos ( − π s ) − i sin ( − π s ) 2 i ) = 1 π s ( 2 i sin ( π s ) 2 i ) = sin ( π s ) π s = s i n c s \begin{aligned}
\mathcal{F} \pi(s)
&= \displaystyle{\int_{-\infty}^{\infty}e^{-2\pi ist}\pi(t)dt } \\
&= \displaystyle{\int_{-\frac{1}{2}}^{\frac{1}{2}}e^{-2\pi ist}dt } \\
&= \left . -\frac{1}{2\pi is}e^{-2\pi ist} \right |_{\frac{1}{2}}^{\frac{1}{2}} \\
&= -\frac{1}{2\pi is}e^{-2\pi is\frac{1}{2}} - (-\frac{1}{2\pi is}e^{-2\pi is(-\frac{1}{2})}) \\
&= -\frac{1}{2\pi is}e^{-\pi is} + \frac{1}{2\pi is}e^{\pi is} \\
&= \frac{1}{\pi s}(\frac{e^{\pi is} - e^{-\pi is}}{2i}) \\
&= \frac{1}{\pi s}(\frac{\cos(\pi s)+i\sin(\pi s) - \cos(-\pi s) - i\sin(-\pi s)}{2i}) \\
&= \frac{1}{\pi s}(\frac{2i\sin(\pi s)}{2i}) \\
&= \frac{\sin(\pi s)}{\pi s} \\
&= sinc \ s
\end{aligned} F π ( s ) = ∫ − ∞ ∞ e − 2 π i s t π ( t ) d t = ∫ − 2 1 2 1 e − 2 π i s t d t = − 2 π i s 1 e − 2 π i s t ∣ ∣ ∣ ∣ 2 1 2 1 = − 2 π i s 1 e − 2 π i s 2 1 − ( − 2 π i s 1 e − 2 π i s ( − 2 1 ) ) = − 2 π i s 1 e − π i s + 2 π i s 1 e π i s = π s 1 ( 2 i e π i s − e − π i s ) = π s 1 ( 2 i cos ( π s ) + i sin ( π s ) − cos ( − π s ) − i sin ( − π s ) ) = π s 1 ( 2 i 2 i sin ( π s ) ) = π s sin ( π s ) = s i n c s
该函数被称为\sinc函数
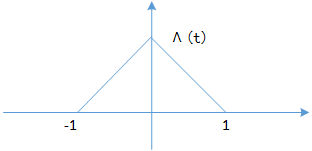
Λ ( t ) = { 1 − ∣ t ∣ ∣ t ∣ < 1 0 ∣ t ∣ ⩾ 1 \Lambda (t) =
\left\{\begin{matrix}
1 - \left|t\right| & \left|t\right|<1 \\
0 & \left|t\right| \geqslant 1
\end{matrix}\right. Λ ( t ) = { 1 − ∣ t ∣ 0 ∣ t ∣ < 1 ∣ t ∣ ⩾ 1
傅里叶变换如下:
F Λ ( s ) = ∫ − ∞ ∞ e − 2 π i s t Λ ( t ) d t = ∫ − 1 0 e − 2 π i s t ( 1 + t ) d t + ∫ 0 1 e − 2 π i s t ( 1 − t ) d t = ( ( 1 + t ) ( − 1 2 π i s e − 2 π i s t ) ∣ − 1 0 − ∫ − 1 0 − 1 2 π i s e − 2 π i s t d t ) + ( ( 1 − t ) ( − 1 2 π i s e − 2 π i s t ) ∣ 0 1 − ∫ 0 1 − 1 2 π i s e − 2 π i s t d t ) = ( − 1 2 π i s − 1 4 π 2 i 2 s 2 e − 2 π i s t ∣ − 1 0 ) + ( 1 2 π i s + 1 4 π 2 i 2 s 2 e − 2 π i s t ∣ 0 1 ) = − ( 1 − 4 π 2 s 2 − 1 − 4 π 2 s 2 e 2 π i s ) + ( 1 − 4 π 2 s 2 e − 2 π i s − 1 − 4 π 2 s 2 ) = − 2 + cos ( 2 π s ) + i sin ( 2 π s ) + cos ( − 2 π s ) + i sin ( − 2 π s ) − 4 π 2 s 2 = − 2 + 2 cos ( 2 π s ) − 4 π 2 s 2 = − 4 sin 2 ( π s ) − 4 π 2 s 2 = sin 2 ( π s ) ( π s ) 2 = s i n c 2 s \begin{aligned}\mathcal{F}\Lambda(s) &= \displaystyle{\int_{-\infty}^{\infty}e^{-2\pi ist}\Lambda(t)dt}\\ &=\displaystyle{\int_{-1}^{0}e^{-2\pi ist}(1+t)dt + \int_{0}^{1}e^{-2\pi ist}(1-t)dt}\\ &=\left(\left.(1+t)(-\frac{1}{2\pi is}e^{-2\pi ist})\right|_{-1}^0-\displaystyle{\int_{-1}^{0}-\frac{1}{2\pi is}e^{-2\pi ist}dt }\right)+\left(\left.(1-t)(-\frac{1}{2\pi is}e^{-2\pi ist})\right|_{0}^1-\displaystyle{\int_{0}^{1}-\frac{1}{2\pi is}e^{-2\pi ist}dt }\right)\\ &=\left(-\frac{1}{2\pi is}-\left. \frac{1}{4\pi^2i^2s^2}e^{-2\pi ist}\right|_{-1}^{0}\right)+\left(\frac{1}{2\pi is}+\left. \frac{1}{4\pi^2i^2s^2}e^{-2\pi ist}\right|_{0}^{1}\right )\\ &=-\left(\frac{1}{-4\pi^2s^2}-\frac{1}{-4\pi^2s^2}e^{2\pi is}\right)+\left(\frac{1}{-4\pi^2s^2}e^{-2\pi is} -\frac{1}{-4\pi^2s^2}\right)\\ &=\frac{-2+\cos(2\pi s)+i\sin(2\pi s)+\cos(-2\pi s)+i\sin(-2\pi s)}{-4\pi^2s^2}\\ &=\frac{-2+2\cos(2\pi s)}{-4\pi^2s^2}\\ &=\frac{-4\sin^2(\pi s)}{-4\pi^2s^2}\\ &=\frac{\sin^2(\pi s)}{(\pi s)^2}\\ &=sinc^2s \end{aligned}
F Λ ( s ) = ∫ − ∞ ∞ e − 2 π i s t Λ ( t ) d t = ∫ − 1 0 e − 2 π i s t ( 1 + t ) d t + ∫ 0 1 e − 2 π i s t ( 1 − t ) d t = ( ( 1 + t ) ( − 2 π i s 1 e − 2 π i s t ) ∣ ∣ ∣ ∣ − 1 0 − ∫ − 1 0 − 2 π i s 1 e − 2 π i s t d t ) + ( ( 1 − t ) ( − 2 π i s 1 e − 2 π i s t ) ∣ ∣ ∣ ∣ 0 1 − ∫ 0 1 − 2 π i s 1 e − 2 π i s t d t ) = ( − 2 π i s 1 − 4 π 2 i 2 s 2 1 e − 2 π i s t ∣ ∣ ∣ ∣ − 1 0 ) + ( 2 π i s 1 + 4 π 2 i 2 s 2 1 e − 2 π i s t ∣ ∣ ∣ ∣ 0 1 ) = − ( − 4 π 2 s 2 1 − − 4 π 2 s 2 1 e 2 π i s ) + ( − 4 π 2 s 2 1 e − 2 π i s − − 4 π 2 s 2 1 ) = − 4 π 2 s 2 − 2 + cos ( 2 π s ) + i sin ( 2 π s ) + cos ( − 2 π s ) + i sin ( − 2 π s ) = − 4 π 2 s 2 − 2 + 2 cos ( 2 π s ) = − 4 π 2 s 2 − 4 sin 2 ( π s ) = ( π s ) 2 sin 2 ( π s ) = s i n c 2 s
傅里叶变换的符号在不同的书籍可能有不同的写法:F f ( s ) \mathcal{F} f(s) F f ( s ) f ^ ( s ) \hat{f}(s) f ^ ( s ) F ( s ) F(s) F ( s ) F − 1 f ( t ) \mathcal{F}^{-1}f(t) F − 1 f ( t ) f ˇ ( t ) \check{f}(t) f ˇ ( t ) f ( t ) f(t) f ( t )
傅里叶变换的公式也没有统一的写法,本课程采用的是如下公式:
F f ( s ) = ∫ − ∞ ∞ e − 2 π i s t f ( t ) d t \mathcal{F} f(s) = \displaystyle{\int_{-\infty}^{\infty}e^{-2\pi ist}f(t)dt }
F f ( s ) = ∫ − ∞ ∞ e − 2 π i s t f ( t ) d t
另外有些书本的写法是:
F f ( s ) = ∫ − ∞ ∞ e − i s t f ( t ) d t \mathcal{F} f(s) = \displaystyle{\int_{-\infty}^{\infty}e^{-ist}f(t)dt }
F f ( s ) = ∫ − ∞ ∞ e − i s t f ( t ) d t
这是由于采用不同的周期而导致的,但是尽管写法不同,但表示的都是同样的意思。
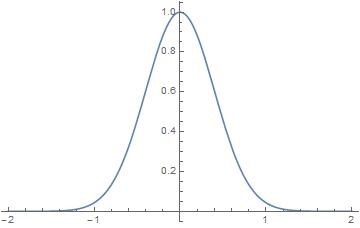
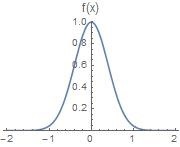
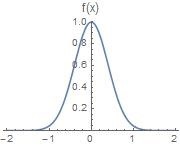
高斯函数的归一化(积分为1)式子如下:f ( t ) = e − π t 2 f(t) = e^{-\pi t^2} f ( t ) = e − π t 2
对高斯函数进行积分过程如下:t t t d t dt d t
( ∫ − ∞ ∞ e − π t 2 d t ) 2 = ∫ − ∞ ∞ e − π x 2 d x × ∫ − ∞ ∞ e − π y 2 d y = ∬ − ∞ ∞ e − π ( x 2 + y 2 ) d x d y = ∫ 0 2 π ∫ 0 ∞ e − π r 2 r d r d θ = 2 π ∫ 0 ∞ e − π r 2 r d r = 2 π ∫ 0 ∞ e − π r 2 d ( 1 2 r 2 ) = 2 π π × 1 2 ∫ 0 ∞ e − π r 2 d π r 2 = ∫ 0 ∞ e − s d s = − e − s ∣ 0 ∞ = 0 − ( − 1 ) = 1 \begin{aligned} \left(\displaystyle{\int_{-\infty}^{\infty}e^{-\pi t^2}dt}\right)^2 &=\displaystyle{\int_{-\infty}^{\infty}e^{-\pi x^2}dx\times \int_{-\infty}^{\infty}e^{-\pi y^2}dy}\\ &=\displaystyle{\iint_{-\infty}^{\infty}e^{-\pi(x^2+y^2)}dxdy}\\ &=\int_0^{2\pi}\int_{0}^{\infty}e^{-\pi r^2}rdrd\theta\\ &=2\pi\int_{0}^{\infty}e^{-\pi r^2}rdr\\ &=2\pi\int_{0}^{\infty}e^{-\pi r^2}d(\frac{1}{2}r^2)\\ &=\frac{2\pi}{\pi}\times\frac{1}{2}\int_0^{\infty}e^{-\pi r^2}d\pi r^2\\ &=\int_0^{\infty}e^{-s}ds\\ &=\left. -e^{-s}\right|_0^{\infty}\\ &=0-(-1)\\ &=1 \end{aligned}
( ∫ − ∞ ∞ e − π t 2 d t ) 2 = ∫ − ∞ ∞ e − π x 2 d x × ∫ − ∞ ∞ e − π y 2 d y = ∬ − ∞ ∞ e − π ( x 2 + y 2 ) d x d y = ∫ 0 2 π ∫ 0 ∞ e − π r 2 r d r d θ = 2 π ∫ 0 ∞ e − π r 2 r d r = 2 π ∫ 0 ∞ e − π r 2 d ( 2 1 r 2 ) = π 2 π × 2 1 ∫ 0 ∞ e − π r 2 d π r 2 = ∫ 0 ∞ e − s d s = − e − s ∣ ∣ 0 ∞ = 0 − ( − 1 ) = 1
那么该高斯函数的积分为
∫ − ∞ ∞ e − π t 2 d t = 1 = 1 \displaystyle{\int_{-\infty}^{\infty}e^{-\pi t^2}dt = \sqrt{1} = 1 }
∫ − ∞ ∞ e − π t 2 d t = 1 = 1
下面对高斯函数进行傅里叶变换
F ( s ) = F f ( s ) = ∫ − ∞ ∞ e − 2 π i s t e − π t 2 d t \begin{aligned} F(s)=\mathcal{F} f(s) &=\int_{-\infty}^{\infty}e^{-2\pi ist}e^{-\pi t^2}dt \end{aligned}
F ( s ) = F f ( s ) = ∫ − ∞ ∞ e − 2 π i s t e − π t 2 d t
这也是一个非常难以积分的项,我们需要采用其他巧妙的方法:微分
F ′ ( s ) = F f ′ ( s ) = ∫ − ∞ ∞ d ( e − 2 π i s t ) d s e − π t 2 d t = ∫ − ∞ ∞ − 2 π i t e − 2 π i s t e − π t 2 d t = i ∫ − ∞ ∞ e − 2 π i s t ( − 2 π t e − π t 2 ) d t = i ( e − 2 π i s t e − π t 2 ∣ − ∞ ∞ − ∫ − ∞ ∞ e − π t 2 ( − 2 π i s e − 2 π i s t ) d t ) = − 2 π s ∫ − ∞ ∞ e − 2 π i s t e − π t 2 d t e l i m i n a t e e − 2 π i s t e − π t 2 ∣ − ∞ ∞ b e c a u s e ∣ e − 2 π i s t ∣ = 1 , lim t → ∞ e − π t 2 = 0 = − 2 π s F ( s ) \begin{aligned} F'(s)=\mathcal{F} f'(s) &=\int_{-\infty}^{\infty}\frac{d(e^{-2\pi ist})}{ds}e^{-\pi t^2}dt\\ &=\int_{-\infty}^{\infty}-2\pi ite^{-2\pi ist}e^{-\pi t^2}dt\\ &=i\int_{-\infty}^{\infty}e^{-2\pi ist}(-2\pi te^{-\pi t^2})dt\\ &=i\left(\left. e^{-2\pi ist}e^{-\pi t^2}\right|_{-\infty}^{\infty}-\int_{-\infty}^{\infty}e^{-\pi t^2}(-2\pi ise^{-2\pi ist})dt\right)\\ &=-2\pi s\int_{-\infty}^{\infty}e^{-2\pi ist}e^{-\pi t^2}dt\qquad eliminate\ \left. e^{-2\pi ist}e^{-\pi t^2}\right|_{-\infty}^{\infty}\ because\ |e^{-2\pi ist}|=1,\lim_{t\to\infty}e^{-\pi t^2}=0\\ &=-2\pi sF(s) \end{aligned}
F ′ ( s ) = F f ′ ( s ) = ∫ − ∞ ∞ d s d ( e − 2 π i s t ) e − π t 2 d t = ∫ − ∞ ∞ − 2 π i t e − 2 π i s t e − π t 2 d t = i ∫ − ∞ ∞ e − 2 π i s t ( − 2 π t e − π t 2 ) d t = i ( e − 2 π i s t e − π t 2 ∣ ∣ ∣ − ∞ ∞ − ∫ − ∞ ∞ e − π t 2 ( − 2 π i s e − 2 π i s t ) d t ) = − 2 π s ∫ − ∞ ∞ e − 2 π i s t e − π t 2 d t e l i m i n a t e e − 2 π i s t e − π t 2 ∣ ∣ ∣ − ∞ ∞ b e c a u s e ∣ e − 2 π i s t ∣ = 1 , t → ∞ lim e − π t 2 = 0 = − 2 π s F ( s )
求偏微分方程,得
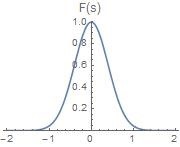
F ( s ) = F ( 0 ) e − π s 2 = ∫ − ∞ ∞ e − π t 2 d t × e − π s 2 = e − π s 2 F(s) = F(0)e^{-\pi s^2} = \displaystyle{\int_{-\infty}^{\infty}e^{-\pi t^2}dt\times e^{-\pi s^2} } = e^{-\pi s^2}
F ( s ) = F ( 0 ) e − π s 2 = ∫ − ∞ ∞ e − π t 2 d t × e − π s 2 = e − π s 2
也就是说归化为1的高斯函数的傅里叶变换还是归化为1的高斯函数
这是一个新的定义,目的是为了方便式子的表达,定义如下f − ( t ) = f ( − t ) f^{-}(t) = f(-t) f − ( t ) = f ( − t ) f − ( t ) f^{-}(t) f − ( t ) f ( t ) f(t) f ( t )
回顾一下傅里叶变换:
F ( s ) = F f ( s ) = ∫ − ∞ ∞ e − 2 π i s t f ( t ) d t F(s) = \mathcal{F} f(s) = \displaystyle{\int_{-\infty}^{\infty}e^{-2\pi ist}f(t)dt }
F ( s ) = F f ( s ) = ∫ − ∞ ∞ e − 2 π i s t f ( t ) d t
当取值为− s -s − s
F ( − s ) = F f ( − s ) = ∫ − ∞ ∞ e 2 π i s t f ( t ) d t = F − 1 f ( s ) F(-s) = \mathcal{F} f(-s) = \displaystyle{\int_{-\infty}^{\infty}e^{2\pi ist}f(t)dt } = \mathcal{F}^{-1}f(s)
F ( − s ) = F f ( − s ) = ∫ − ∞ ∞ e 2 π i s t f ( t ) d t = F − 1 f ( s )
一般来说,f ( t ) f(t) f ( t ) F ( s ) F(s) F ( s ) f ( t ) f(t) f ( t ) F ( s ) F(s) F ( s ) F ( s ) F(s) F ( s ) f ( t ) f(t) f ( t ) f ( t ) f(t) f ( t )
把反转信号引入傅里叶变换的对偶性中,得F f ( − s ) = ( F f ) − ( s ) \mathcal{F} f(-s) = (\mathcal{F} f)^{-}(s) F f ( − s ) = ( F f ) − ( s ) F f ( − s ) = F − 1 f ( s ) \mathcal{F} f(-s) = \mathcal{F}^{-1}f(s) F f ( − s ) = F − 1 f ( s )
( F f ) − ( s ) = F − 1 f ( s ) (\mathcal{F} f)^{-}(s) = \mathcal{F}^{-1}f(s)
( F f ) − ( s ) = F − 1 f ( s )
( F f ) − = F − f (\mathcal{F} f)^{-} = \mathcal{F}^{-}f
( F f ) − = F − f
函数的傅里叶变换的反转等于对该函数进行傅里叶逆变换。
如果对f − ( t ) f^{-}(t) f − ( t )
F ( f − ( s ) ) = ∫ − ∞ ∞ e − 2 π i s t f ( − t ) d t = ∫ + ∞ − ∞ e − 2 π i s ( − u ) f ( u ) d ( − u ) l e t u = − t = ∫ − ∞ ∞ e 2 π i s u f ( u ) d u = F − 1 f ( s ) \begin{aligned}
\mathcal{F}(f^{-}(s))
&= \int_{-\infty}^{\infty}e^{-2\pi ist}f(-t)dt\\
&= \int_{+\infty}^{-\infty}e^{-2\pi is(-u)}f(u)d(-u) \qquad let \ u=-t\\
&= \int_{-\infty}^{\infty}e^{2\pi isu}f(u)du\\
&= \mathcal{F}^{-1}f(s)
\end{aligned} F ( f − ( s ) ) = ∫ − ∞ ∞ e − 2 π i s t f ( − t ) d t = ∫ + ∞ − ∞ e − 2 π i s ( − u ) f ( u ) d ( − u ) l e t u = − t = ∫ − ∞ ∞ e 2 π i s u f ( u ) d u = F − 1 f ( s )
即,
F ( f − ) = F − f \mathcal{F}(f^{-}) = \mathcal{F}^{-}f
F ( f − ) = F − f
函数的反转的傅里叶变换等于对该函数进行傅里叶逆变换。
把对偶定理1与对偶定理2结合起来,得
( F f ) − = F ( f − ) (\mathcal{F} f)^{-} = \mathcal{F}(f^{-})
( F f ) − = F ( f − )
函数的傅里叶变换的反转等于对该函数反转的傅里叶变换
对函数进行两次傅里叶变换
F F f = F ( F f ) = F ( F − ( f − ) ) = f − \mathcal{F}\mathcal{F} f = \mathcal{F}(\mathcal{F} f) = \mathcal{F} (\mathcal{F}^{-}(f^{-})) = f^{-}
F F f = F ( F f ) = F ( F − ( f − ) ) = f −
函数连续进行两次傅里叶变换等于该函数的反转。
对偶定理的目的是为了方便计算,如求\sinc函数的傅里叶变换。
\sinc = \frac{\sin \pi s}{\pi s}
由上一节课我们知道π \pi π
\mathcal{F} \sinc = \mathcal{F}\mathcal{F} \pi = \pi^{-} = \pi
在傅里叶变换中有时域f ( t ) f(t) f ( t ) F ( s ) F(s) F ( s ) f ( t ) ↔ F ( s ) f(t) \ \leftrightarrow \ F(s) f ( t ) ↔ F ( s )
f ( t − b ) ↔ ? f(t-b) \ \leftrightarrow \ ?
f ( t − b ) ↔ ?
时延性在时域的表示为f ( t − b ) f(t-b) f ( t − b ) f ( t ) f(t) f ( t )
∫ − ∞ ∞ e − 2 π i s t f ( t − b ) d t = ∫ − ∞ ∞ e − 2 π i s ( u + b ) f ( u ) d u u = t − b = ∫ − ∞ ∞ e − 2 π i s u e − 2 π i s b f ( u ) d u = e − 2 π i s b ∫ − ∞ ∞ e − 2 π i s u f ( u ) d u = e − 2 π i s b F ( s ) \begin{aligned}
&\quad \int_{-\infty}^{\infty}e^{-2\pi ist}f(t-b)dt\\
&=\int_{-\infty}^{\infty}e^{-2\pi is(u+b)}f(u)du \quad u=t-b\\
&=\int_{-\infty}^{\infty}e^{-2\pi isu}e^{-2\pi isb}f(u)du\\
&=e^{-2\pi isb}\int_{-\infty}^{\infty}e^{-2\pi isu}f(u)du\\
&=e^{-2\pi isb}F(s)
\end{aligned} ∫ − ∞ ∞ e − 2 π i s t f ( t − b ) d t = ∫ − ∞ ∞ e − 2 π i s ( u + b ) f ( u ) d u u = t − b = ∫ − ∞ ∞ e − 2 π i s u e − 2 π i s b f ( u ) d u = e − 2 π i s b ∫ − ∞ ∞ e − 2 π i s u f ( u ) d u = e − 2 π i s b F ( s )
因此,
f ( t − b ) ↔ e − 2 π i s b F ( s ) f(t-b)\leftrightarrow e^{-2\pi isb}F(s)
f ( t − b ) ↔ e − 2 π i s b F ( s )
f ( t ± b ) ↔ e ± 2 π i s b F ( s ) f(t\pm b)\leftrightarrow e^{\pm 2\pi isb}F(s)
f ( t ± b ) ↔ e ± 2 π i s b F ( s )
时域上的时移对应频域上的相移(Shift in time corresponds to a phase shift in frequency)。令F ( s ) = ∣ F ( s ) ∣ e 2 π i θ ( s ) F(s) = |F(s)|e^{2\pi i\theta(s)} F ( s ) = ∣ F ( s ) ∣ e 2 π i θ ( s ) ∣ F ( s ) ∣ |F(s)| ∣ F ( s ) ∣ θ ( s ) \theta(s) θ ( s )
e − 2 π i s b F ( s ) = ∣ F ( s ) ∣ e 2 π i ( θ ( s ) − s b ) e^{-2\pi isb}F(s)=|F(s)|e^{2\pi i(\theta(s)-sb)}
e − 2 π i s b F ( s ) = ∣ F ( s ) ∣ e 2 π i ( θ ( s ) − s b )
上面的等式代表了频谱的振幅不变,而相位改变了。
f ( a t ) ↔ ? f(at) \ \leftrightarrow \ ?
f ( a t ) ↔ ?
a > 0 a>0 a > 0 ∫ − ∞ ∞ e − 2 π i s t f ( a t ) d t = ∫ − ∞ ∞ e − 2 π i s ( u a ) f ( u ) d u a u = a t = 1 a ∫ − ∞ ∞ e − 2 π i ( s a ) u f ( u ) d u = 1 a F ( s a ) \begin{aligned}
&\quad \int_{-\infty}^{\infty}e^{-2\pi ist}f(at)dt\\
&=\int_{-\infty}^{\infty}e^{-2\pi is(\frac{u}{a})}f(u)d\frac{u}{a} \quad u=at\\
&=\frac{1}{a}\int_{-\infty}^{\infty}e^{-2\pi i(\frac{s}{a})u}f(u)du\\
&=\frac{1}{a}F(\frac{s}{a})
\end{aligned} ∫ − ∞ ∞ e − 2 π i s t f ( a t ) d t = ∫ − ∞ ∞ e − 2 π i s ( a u ) f ( u ) d a u u = a t = a 1 ∫ − ∞ ∞ e − 2 π i ( a s ) u f ( u ) d u = a 1 F ( a s )
a < 0 a<0 a < 0 ∫ − ∞ ∞ e − 2 π i s t f ( a t ) d t = ∫ − ∞ ∞ e − 2 π i s ( u a ) f ( u ) d u a u = a t = 1 a ∫ ∞ − ∞ e − 2 π i ( s a ) u f ( u ) d u = − 1 a ∫ − ∞ ∞ e − 2 π i ( s a ) u f ( u ) d u = − 1 a F ( s a ) \begin{aligned}
&\quad \int_{-\infty}^{\infty}e^{-2\pi ist}f(at)dt\\
&=\int_{-\infty}^{\infty}e^{-2\pi is(\frac{u}{a})}f(u)d\frac{u}{a} \quad u=at\\
&=\frac{1}{a}\int_{\infty}^{-\infty}e^{-2\pi i(\frac{s}{a})u}f(u)du\\
&=-\frac{1}{a}\int_{-\infty}^{\infty}e^{-2\pi i(\frac{s}{a})u}f(u)du\\
&=-\frac{1}{a}F(\frac{s}{a})
\end{aligned} ∫ − ∞ ∞ e − 2 π i s t f ( a t ) d t = ∫ − ∞ ∞ e − 2 π i s ( a u ) f ( u ) d a u u = a t = a 1 ∫ ∞ − ∞ e − 2 π i ( a s ) u f ( u ) d u = − a 1 ∫ − ∞ ∞ e − 2 π i ( a s ) u f ( u ) d u = − a 1 F ( a s )
把两种情况合在一起,有
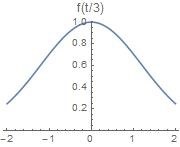
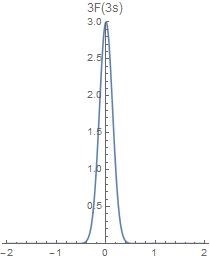
f ( a t ) ↔ 1 ∣ a ∣ F ( s a ) f(at) \ \leftrightarrow \ \frac{1}{|a|}F(\frac{s}{a})
f ( a t ) ↔ ∣ a ∣ 1 F ( a s )
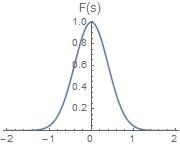
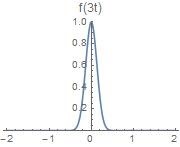
下面在图像上观察时域与频域具体是如何变化的(以高斯函数为例子)
a > 1 a>1 a > 1 时域横向压缩,频域横向扩展、纵向压缩,即频域分散
0 < a < 1 0 0 < a < 1 时域横向扩展,频域横向压缩、纵向扩展,即频域集中
卷积可能算是信号处理中最重要的运算了。信号处理可以被理解为:如何用一个函数(信号)调制另一个函数(信号)。(Signal Processing can be said to how can you use one function(signal) to modify another.)大部分情况下,信号处理是着力于改变信号的频谱,也就是说,先对信号进行傅里叶变换,然后在频域进行处理,之和进行傅里叶逆变换得到处理过后的信号。
即两个信号线性叠加
F ( f + g ) = ∫ − ∞ ∞ e − 2 π i s t ( f ( t ) + g ( t ) ) d t = ∫ − ∞ ∞ ( e − 2 π i s t f ( t ) + e − 2 π i s t g ( t ) ) d t = ∫ − ∞ ∞ e − 2 π i s t f ( t ) d t + ∫ − ∞ ∞ e − 2 π i s t g ( t ) d t = F f + F g \begin{aligned} \mathcal{F}(f+g) &=\int_{-\infty}^{\infty}e^{-2\pi ist}(f(t)+g(t))dt\\ &=\int_{-\infty}^{\infty}\left(e^{-2\pi ist}f(t)+e^{-2\pi ist}g(t)\right)dt\\ &=\int_{-\infty}^{\infty}e^{-2\pi ist}f(t)dt+\int_{-\infty}^{\infty}e^{-2\pi ist}g(t)dt\\ &=\mathcal{F} f + \mathcal{F} g \end{aligned}
F ( f + g ) = ∫ − ∞ ∞ e − 2 π i s t ( f ( t ) + g ( t ) ) d t = ∫ − ∞ ∞ ( e − 2 π i s t f ( t ) + e − 2 π i s t g ( t ) ) d t = ∫ − ∞ ∞ e − 2 π i s t f ( t ) d t + ∫ − ∞ ∞ e − 2 π i s t g ( t ) d t = F f + F g
F ( f ) F ( g ) = ∫ − ∞ ∞ e − 2 π i s t g ( t ) d t ∫ − ∞ ∞ e − 2 π i s x g ( x ) d x = ∬ − ∞ ∞ e − 2 π i s t e − 2 π i s x g ( t ) f ( x ) d t d x = ∬ − ∞ ∞ e − 2 π i s ( t + x ) g ( t ) f ( x ) d t d x = ∫ − ∞ ∞ ( ∫ − ∞ ∞ e − 2 π i s ( t + x ) g ( t ) d t ) f ( x ) d x = ∫ − ∞ ∞ ( ∫ − ∞ ∞ e − 2 π i s ( u ) g ( u − x ) d u ) f ( x ) d x u = t + x = ∫ − ∞ ∞ ( ∫ − ∞ ∞ g ( u − x ) f ( x ) d x ) e − 2 π i s u d u \begin{aligned}
\mathcal{F}(f)\mathcal{F}(g)
&=\int_{-\infty}^{\infty}e^{-2\pi ist}g(t)dt\int_{-\infty}^{\infty}e^{-2\pi isx}g(x)dx\\
&=\iint_{-\infty}^{\infty}e^{-2\pi ist}e^{-2\pi isx}g(t)f(x)dtdx\\
&=\iint_{-\infty}^{\infty}e^{-2\pi is(t+x)}g(t)f(x)dtdx\\
&=\int_{-\infty}^{\infty}\left(\int_{-\infty}^{\infty}e^{-2\pi is(t+x)}g(t)dt \right )f(x)dx\\
&=\int_{-\infty}^{\infty}\left(\int_{-\infty}^{\infty}e^{-2\pi is(u)}g(u-x)du \right )f(x)dx \quad u=t+x\\
&=\int_{-\infty}^{\infty}\left(\int_{-\infty}^{\infty}g(u-x)f(x)dx \right )e^{-2\pi isu}du\\
\end{aligned} F ( f ) F ( g ) = ∫ − ∞ ∞ e − 2 π i s t g ( t ) d t ∫ − ∞ ∞ e − 2 π i s x g ( x ) d x = ∬ − ∞ ∞ e − 2 π i s t e − 2 π i s x g ( t ) f ( x ) d t d x = ∬ − ∞ ∞ e − 2 π i s ( t + x ) g ( t ) f ( x ) d t d x = ∫ − ∞ ∞ ( ∫ − ∞ ∞ e − 2 π i s ( t + x ) g ( t ) d t ) f ( x ) d x = ∫ − ∞ ∞ ( ∫ − ∞ ∞ e − 2 π i s ( u ) g ( u − x ) d u ) f ( x ) d x u = t + x = ∫ − ∞ ∞ ( ∫ − ∞ ∞ g ( u − x ) f ( x ) d x ) e − 2 π i s u d u
令h ( u ) = ∫ − ∞ ∞ g ( u − x ) f ( x ) d x h(u) = \displaystyle{\int_{-\infty}^{\infty}g(u-x)f(x)dx } h ( u ) = ∫ − ∞ ∞ g ( u − x ) f ( x ) d x
( F g ) ( F f ) = ∫ − ∞ ∞ e − 2 π i s u h ( u ) d u (\mathcal{F} g)(\mathcal{F} f) = \displaystyle{\int_{-\infty}^{\infty}e^{-2\pi isu}h(u)du }
( F g ) ( F f ) = ∫ − ∞ ∞ e − 2 π i s u h ( u ) d u
卷积用符号∗表示,运算方法如下
( g ∗ f ) ( x ) = ∫ − ∞ ∞ g ( x − y ) f ( y ) d y (g*f)(x) = \displaystyle{\int_{-\infty}^{\infty}g(x-y)f(y)dy }
( g ∗ f ) ( x ) = ∫ − ∞ ∞ g ( x − y ) f ( y ) d y
F ( g ∗ f ) = ( F g ) ( F f ) \mathcal{F}(g*f) = (\mathcal{F} g)(\mathcal{F} f)
F ( g ∗ f ) = ( F g ) ( F f )
信号的卷积的傅里叶变换等于对这些信号进行傅里叶变换后的乘积。
浑浊度(Turbidity)研究是关于测量水的清澈度的研究。大致方法是把光传感器放置到深水区域,然后测量光线的昏暗程度,测量出来的值将随时间变化。(由于没有真实数据,下面用mathematica比较粗糙地模拟水域的浑浊度数据)
能看到信号主要集中在低频,我们需要把毛刺去除,也就是把高频去除,在频域进行低通滤波(Low Pass Filtering)
滤波后的波形如下
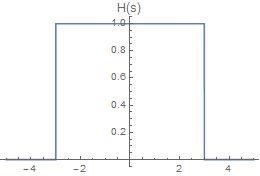
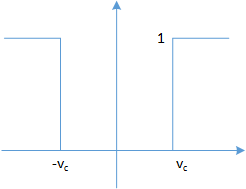
频域运算:π 2 ν c F ( s ) \pi_{2\nu_c} F(s) π 2 ν c F ( s )
滤波(Filtering) 通常等同于卷积,滤波是由滤波器实现的。滤波器(Filter) 是一个输入可变的函数(信号)与一个固定的函数(信号)进行卷积运算的系统。这个固定的信号叫做脉冲响应(impulse response)。
g = f ∗ h g \quad = \quad f \qquad * \qquad h
g = f ∗ h
o u t p u t i n p u t i m p u l s e r e s p o n s e \qquad output \qquad input \qquad impulse \ response
o u t p u t i n p u t i m p u l s e r e s p o n s e
卷积是在时域的表示方法,一般来说,频域的运算会比时域简单许多,因为频域只需执行相乘运算。
G ( s ) = F ( s ) H ( s ) G(s) = F(s)H(s)
G ( s ) = F ( s ) H ( s )
H ( s ) H(s) H ( s ) H ( s ) H(s) H ( s )
高通滤波器(high pass filter),常用于边缘检测(edge detection)
带通滤波器(band pass filter)
教授认为只需要从频域理解为函数的相乘即可,而在时域上不需要去具象化卷积。(I think it is equally idiotic to try to visualize convolution. I think the way to visualize convolution, if there is a way, is to think in terms of multiplying in the frequency domain.)
一般来说f ∗ g f*g f ∗ g f f f g g g Π \Pi Π Π \Pi Π Λ \Lambda Λ
\mathcal{F}(\Pi * \Pi) = (\mathcal{F} \Pi)(\mathcal{F} \Pi) = \sinc^2 = \mathcal{F} \Lambda
对原函数进行微分后,它的傅里叶变换等于其原函数的傅里叶变换乘以F ( f ′ ) ( s ) = 2 π i s ( F f ) ( s ) \mathcal{F}(f')(s) = 2\pi is(\mathcal{F} f)(s) F ( f ′ ) ( s ) = 2 π i s ( F f ) ( s )
f ( t ) = ∫ − ∞ ∞ F ( s ) e 2 π i s t d s f(t) = \displaystyle{\int_{-\infty}^{\infty} F(s)e^{2\pi ist}ds }
f ( t ) = ∫ − ∞ ∞ F ( s ) e 2 π i s t d s
对其求微分,
∂ f ∂ t = ∫ − ∞ ∞ F ( s ) ( 2 π i s e 2 π i s t ) d s = ∫ − ∞ ∞ ( 2 π i s F ( s ) ) e 2 π i s t d s \begin{aligned}
\frac{\partial f}{\partial t}
&= \int_{-\infty}^{\infty}F(s)(2\pi ise^{2\pi ist})ds \\
&= \int_{-\infty}^{\infty}(2\pi isF(s))e^{2\pi ist}ds \\
\end{aligned} ∂ t ∂ f = ∫ − ∞ ∞ F ( s ) ( 2 π i s e 2 π i s t ) d s = ∫ − ∞ ∞ ( 2 π i s F ( s ) ) e 2 π i s t d s
则有f ′ f' f ′ 2 π i s F ( s ) 2\pi isF(s) 2 π i s F ( s )
f ′ ↔ 2 π i s F ( s ) f' \ \leftrightarrow \ 2\pi isF(s)
f ′ ↔ 2 π i s F ( s )
推广开来有
F ( f n ) ( s ) = ( 2 π i s ) n ( F f ) ( s ) \mathcal{F}(f^n)(s) = (2\pi is)^n(\mathcal{F} f)(s)
F ( f n ) ( s ) = ( 2 π i s ) n ( F f ) ( s )
U ( x , t ) U(x,t) U ( x , t ) t t t x x x
已知初始温度为U ( x , 0 ) = f ( x ) U(x,0) = f(x) U ( x , 0 ) = f ( x ) U t = 1 2 U x x U_t = \frac{1}{2}U_{xx} U t = 2 1 U x x U ( x , t ) U(x,t) U ( x , t ) x x x U ( s , t ) U(s,t) U ( s , t )
F ( U t ) = ∫ − ∞ ∞ e − 2 π i s x ∂ ∂ t U ( x , t ) d x = ∂ ∂ t ∫ − ∞ ∞ e − 2 π i s x U ( x , t ) d x = ∂ ∂ t U ( s , t ) \begin{aligned}
\mathcal{F}(U_t)
&= \int_{-\infty}^{\infty}e^{-2\pi isx} \frac{\partial}{\partial t}U(x,t)dx \\
&= \frac{\partial}{\partial t}\int_{-\infty}^{\infty} e^{-2\pi isx}U(x,t)dx \\
&= \frac{\partial}{\partial t}U(s,t)
\end{aligned} F ( U t ) = ∫ − ∞ ∞ e − 2 π i s x ∂ t ∂ U ( x , t ) d x = ∂ t ∂ ∫ − ∞ ∞ e − 2 π i s x U ( x , t ) d x = ∂ t ∂ U ( s , t )
对热方程等号右边进行傅里叶变换,
F ( 1 2 U x x ) = 1 2 ( 2 π i s ) 2 U ( s , t ) = − 2 π 2 s 2 U ( s , t ) \mathcal{F}(\frac{1}{2}U_{xx}) = \frac{1}{2}(2\pi is)^2U(s,t) = -2\pi ^2s^2U(s,t)
F ( 2 1 U x x ) = 2 1 ( 2 π i s ) 2 U ( s , t ) = − 2 π 2 s 2 U ( s , t )
即有
∂ ∂ t U ( s , t ) = − 2 π 2 s 2 U ( s , t ) \frac{\partial}{\partial t}U(s,t) = -2\pi^2s^2U(s,t)
∂ t ∂ U ( s , t ) = − 2 π 2 s 2 U ( s , t )
求偏微分方程,得
U ( s , t ) = U ( s , 0 ) e − 2 π 2 s 2 t U(s,t) = U(s,0)e^{-2\pi^2s^2t}
U ( s , t ) = U ( s , 0 ) e − 2 π 2 s 2 t
U ( s , 0 ) = ∫ − ∞ ∞ U ( x , 0 ) e − 2 π i s x d x = ∫ − ∞ ∞ f ( x ) e − 2 π i s x d x = F ( s ) U(s,0) = \displaystyle{\int_{-\infty}^{\infty}U(x,0)e^{-2\pi isx}dx=\int_{-\infty}^{\infty}f(x)e^{-2\pi isx}dx = F(s) }
U ( s , 0 ) = ∫ − ∞ ∞ U ( x , 0 ) e − 2 π i s x d x = ∫ − ∞ ∞ f ( x ) e − 2 π i s x d x = F ( s )
把U ( s , 0 ) U(s,0) U ( s , 0 ) U ( s , t ) U(s,t) U ( s , t )
U ( s , t ) = F ( s ) e − 2 π 2 s 2 t U(s,t) = F(s)e^{-2\pi ^2s^2t}
U ( s , t ) = F ( s ) e − 2 π 2 s 2 t
转换为卷积格式
e − 2 p i 2 s 2 t = F ( 1 2 π t e x 2 2 t ) e^{-2pi ^2s^2t} = \mathcal{F}(\frac{1}{\sqrt{2\pi t}}e^{\frac{x^2}{2t}})
e − 2 p i 2 s 2 t = F ( 2 π t 1 e 2 t x 2 )
U ( s , t ) = F ( s ) e − 2 π 2 s 2 t = ( F f ) ( F ( 1 2 π t e x 2 2 t ) ) = F ( f ∗ 1 2 π t e x 2 2 t ) \begin{aligned}
U(s,t)
&= F(s)e^{-2\pi ^2s^2t}\\
&= (\mathcal{F} f)(\mathcal{F} (\frac{1}{\sqrt{2\pi t}}e^{\frac{x^2}{2t}}))\\
&= \mathcal{F}(f* \frac{1}{\sqrt{2\pi t}}e^{\frac{x^2}{2t}})
\end{aligned} U ( s , t ) = F ( s ) e − 2 π 2 s 2 t = ( F f ) ( F ( 2 π t 1 e 2 t x 2 ) ) = F ( f ∗ 2 π t 1 e 2 t x 2 )
U ( x , t ) = f ( x ) ∗ 1 2 π t e x 2 2 t U(x,t) = f(x) * \frac{1}{\sqrt{2\pi t}}e^{\frac{x^2}{2t}}
U ( x , t ) = f ( x ) ∗ 2 π t 1 e 2 t x 2
中心极限定理,简称CLT。大多数概率事件,当有足够多的取样时,都服从高斯分布。(Most probabilities - some kind of average - are calculated or approximated as if they are determined by a Gaussian.)
在傅里叶变换中,我们用f = e − π t 2 f = e^{-\pi t^2} f = e − π t 2 e − π t 2 e^{-\pi t^2} e − π t 2
p ( x ) = 1 2 π e − x 2 2 p(x) = \frac{1}{\sqrt{2\pi}} e^{\frac{-x^2}{2}}
p ( x ) = 2 π 1 e 2 − x 2
采用这个式子作为标准正态分布的原因是它的均值(期望值)是0,它的标准差与方差为1。对应地,概率函数为
P r o b ( a ⩽ X ⩽ b ) = ∫ a b p ( x ) d x = 1 2 π ∫ a b e − x 2 2 d x Prob(a \leqslant X \leqslant b) = \displaystyle{\int_a^b p(x) dx = \frac{1}{\sqrt{2\pi}}\int_a^b e^{-\frac{x^2}{2}}dx }
P r o b ( a ⩽ X ⩽ b ) = ∫ a b p ( x ) d x = 2 π 1 ∫ a b e − 2 x 2 d x
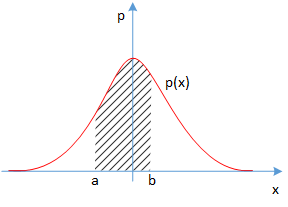
设有随机变量X X X X X X X X X x x x x x x p ( x ) p(x) p ( x ) x x x
p ( x ) ⩾ 0 p(x) \geqslant 0
p ( x ) ⩾ 0
x x x a a a b b b
P r o b ( a ⩽ x ⩽ b ) = ∫ a b p ( x ) d x Prob(a \leqslant x \leqslant b) = \displaystyle{\int_a^b p(x)dx }
P r o b ( a ⩽ x ⩽ b ) = ∫ a b p ( x ) d x
总概率为1
P r o b ( − ∞ ⩽ x ⩽ ∞ ) = ∫ − ∞ ∞ p ( x ) d x = 1 Prob(-\infty \leqslant x \leqslant \infty) = \displaystyle{\int_{-\infty}^{\infty}p(x)dx = 1 }
P r o b ( − ∞ ⩽ x ⩽ ∞ ) = ∫ − ∞ ∞ p ( x ) d x = 1
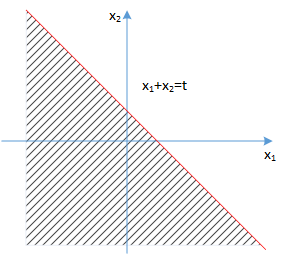
假设有两个独立的随机变量:x 1 x_1 x 1 x 2 x_2 x 2 p 1 ( x 1 ) p_1(x_1) p 1 ( x 1 ) p 2 ( x 2 ) p_2(x_2) p 2 ( x 2 ) x 1 + x 2 x_1+x_2 x 1 + x 2 p 12 ( x 12 ) p_{12}(x_{12}) p 1 2 ( x 1 2 ) p 1 ( x 1 ) p_1(x_1) p 1 ( x 1 ) p 2 ( x 2 ) p_2(x_2) p 2 ( x 2 ) t t t x 1 + x 2 ⩽ t x_1+x_2 \leqslant t x 1 + x 2 ⩽ t P r o b ( x 1 + x 2 ⩽ t ) Prob(x_1+x_2 \leqslant t) P r o b ( x 1 + x 2 ⩽ t )
P r o b ( x 1 + x 2 ⩽ t ) Prob(x_1+x_2 \leqslant t) P r o b ( x 1 + x 2 ⩽ t )
P r o b ( x x + x 2 ⩽ t ) = ∬ x 1 + x 2 ⩽ t p 1 ( x 1 ) p 2 ( x 2 ) d x 1 d x 2 Prob(x_x+x_2 \leqslant t) = \displaystyle{\iint_{x_1 + x_2 \leqslant t} p_1(x_1)p_2(x_2)dx_1dx_2 }
P r o b ( x x + x 2 ⩽ t ) = ∬ x 1 + x 2 ⩽ t p 1 ( x 1 ) p 2 ( x 2 ) d x 1 d x 2
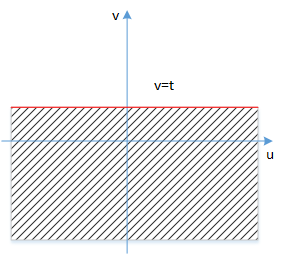
进行变量代换,令u = x 1 u=x_1 u = x 1 v = x 1 + x 2 v=x_1+x_2 v = x 1 + x 2
{ x 1 = u x 2 = v − u t = v \left\{\begin{matrix}
x_1 &= &u\\
x_2 &= &v - u\\
t &= &v
\end{matrix}\right. ⎩ ⎨ ⎧ x 1 x 2 t = = = u v − u v
进行变量代换后,对应的新平面(u u u v v v
计算如下
P r o b ( x 1 + x 2 ⩽ t ) = P r o b ( v ⩽ t ) = ∫ − ∞ ∞ ∫ − ∞ t p 1 ( u ) p 2 ( v − u ) d u d v = ∫ − ∞ t ( ∫ − ∞ ∞ p 1 ( u ) p 2 ( v − u ) d u ) d v = ∫ − ∞ t ( p 1 ∗ p 2 ) d v \begin{aligned}
Prob(x_1+x_2 \leqslant t)
&= Prob(v \leqslant t) \\
&= \int_{-\infty}^{\infty}\int_{-\infty}^{t}p_1(u)p_2(v-u)dudv \\
&= \int_{-\infty}^{t}\left( \int_{-\infty}^{\infty}p_1(u)p_2(v-u)du \right)dv \\
&= \int_{-\infty}^{t}(p_1 * p_2)dv
\end{aligned} P r o b ( x 1 + x 2 ⩽ t ) = P r o b ( v ⩽ t ) = ∫ − ∞ ∞ ∫ − ∞ t p 1 ( u ) p 2 ( v − u ) d u d v = ∫ − ∞ t ( ∫ − ∞ ∞ p 1 ( u ) p 2 ( v − u ) d u ) d v = ∫ − ∞ t ( p 1 ∗ p 2 ) d v
因此p 1 ∗ p 2 p_1 * p_2 p 1 ∗ p 2 x 1 + x 2 x_1+x_2 x 1 + x 2
p ( x 1 + x 2 + … + x n ) = p 1 ∗ p 2 ∗ … ∗ p n p(x_1+x_2+…+x_n) = p_1*p_2*…*p_n
p ( x 1 + x 2 + … + x n ) = p 1 ∗ p 2 ∗ … ∗ p n
设有n n n x 1 , x 2 , … , x n x_1,x_2,…,x_n x 1 , x 2 , … , x n
有相同的密度函数:p 1 = p 2 = … = p n = p ( x ) p_1=p_2=…=p_n=p(x) p 1 = p 2 = … = p n = p ( x )
均值(期望值)为:μ = ∫ − ∞ ∞ x p ( x ) d x = 0 \mu = \displaystyle{\int_{-\infty}^{\infty}xp(x)dx=0 } μ = ∫ − ∞ ∞ x p ( x ) d x = 0
标准差为:σ = ∫ − ∞ ∞ x 2 p ( x ) d x = 1 \sigma = \displaystyle{\sqrt{\int_{-\infty}^{\infty}x^2p(x)dx } =1} σ = ∫ − ∞ ∞ x 2 p ( x ) d x = 1
概率的一般性质,总概率为:∫ − ∞ ∞ p ( x ) d x = 1 \displaystyle{\int_{-\infty}^{\infty}p(x)dx = 1 } ∫ − ∞ ∞ p ( x ) d x = 1
设S n S_n S n n n n
S n = x 1 + x 2 + . . . + x n S_n = x_1+x_2+...+x_n
S n = x 1 + x 2 + . . . + x n
S n S_n S n
p ∗ n = p ∗ p ∗ . . . ∗ p ⏟ n p^{*n} = \underbrace{p*p*...*p}_n
p ∗ n = n p ∗ p ∗ . . . ∗ p
S n S_n S n 0 0 0 n \sqrt{n} n
横轴缩放。标准化后密度函数为f ( z ) f(z) f ( z ) z = x − μ σ z = \frac{x-\mu}{\sigma} z = σ x − μ x = σ z + μ = n z x=\sigma z+\mu = \sqrt{n}z x = σ z + μ = n z
纵轴缩放。f ( z ) = σ f ( x ) = n p ∗ n ( x ) f(z) = \sigma f(x) = \sqrt{n} p^{*n}(x) f ( z ) = σ f ( x ) = n p ∗ n ( x )
两个步骤合在一起,得到
f ( z ) = n p ∗ n ( n z ) f(z) = \sqrt{n} p^{*n}(\sqrt{n}z)
f ( z ) = n p ∗ n ( n z )
记标准化后的密度函数为
p n o r m a l ( x ) = n p ∗ n ( n x ) p_{normal}(x) = \sqrt{n} p^{*n}(\sqrt{n}x)
p n o r m a l ( x ) = n p ∗ n ( n x )
为了把卷积计算简化,需要引入傅里叶变换把卷积运算转换为乘法运算
F ( n ( p ∗ n ) ( n x ) ) = n ⋅ 1 n ( F ( p ∗ n ) ) ( s n ) F o u r i e r S c a l i n g T h e o r e m = ( F ( p ∗ n ) ) ( s n ) = ( F p ) n ( s n ) F o u r i e r C o n v o l u t i o n T h e o r e m = ( ∫ − ∞ ∞ e − 2 π i ( s n ) x p ( x ) d x ) n = ( ∫ − ∞ ∞ ( 1 − 2 π i s x n + 1 2 ( 2 π i s x n ) 2 + . . . ) p ( x ) d x ) n T a y l o r S e r i e s = ( ∫ − ∞ ∞ p ( x ) d x − 2 π i s n ∫ − ∞ ∞ x p ( x ) d x − 2 π 2 s 2 n ∫ − ∞ ∞ x 2 p ( x ) d x + . . . ) n = ( 1 − 0 − 2 π 2 s 2 n + . . . ) n ≈ ( 1 − 2 π 2 s 2 n ) n \begin{aligned}
\mathcal{F}\left(\sqrt{n}(p^{*n})(\sqrt{n}x)\right)
&=\sqrt{n}\cdot\frac{1}{\sqrt{n}}\left(\mathcal{F}(p^{*n})\right)(\frac{s}{\sqrt{n}})\quad Fourier\ Scaling\ Theorem\\
&=(\mathcal{F}(p^{*n}))(\frac{s}{\sqrt{n}})\\
&=(\mathcal{F} p)^n(\frac{s}{\sqrt{n}})\quad Fourier\ Convolution\ Theorem\\
&=\left(\int_{-\infty}^{\infty}e^{-2\pi i(\frac{s}{\sqrt{n}})x} p(x)dx\right)^n\\
&=\left(\int_{-\infty}^{\infty}\left(1-\frac{2\pi isx}{\sqrt{n}}+\frac{1}{2}\left(\frac{2\pi isx}{\sqrt{n}}\right)^2+...\right)p(x)dx\right)^n\quad Taylor \ Series\\
&=\left(\int_{-\infty}^{\infty}p(x)dx-\frac{2\pi is}{\sqrt{n}}\int_{-\infty}^{\infty}xp(x)dx-\frac{2\pi^2s^2}{n}\int_{-\infty}^{\infty}x^2p(x)dx+...\right)^n\\
&=\left(1-0-\frac{2\pi^2s^2}{n}+...\right)^n\\
&\approx\left(1-\frac{2\pi^2s^2}{n}\right)^n
\end{aligned} F ( n ( p ∗ n ) ( n x ) ) = n ⋅ n 1 ( F ( p ∗ n ) ) ( n s ) F o u r i e r S c a l i n g T h e o r e m = ( F ( p ∗ n ) ) ( n s ) = ( F p ) n ( n s ) F o u r i e r C o n v o l u t i o n T h e o r e m = ( ∫ − ∞ ∞ e − 2 π i ( n s ) x p ( x ) d x ) n = ( ∫ − ∞ ∞ ( 1 − n 2 π i s x + 2 1 ( n 2 π i s x ) 2 + . . . ) p ( x ) d x ) n T a y l o r S e r i e s = ( ∫ − ∞ ∞ p ( x ) d x − n 2 π i s ∫ − ∞ ∞ x p ( x ) d x − n 2 π 2 s 2 ∫ − ∞ ∞ x 2 p ( x ) d x + . . . ) n = ( 1 − 0 − n 2 π 2 s 2 + . . . ) n ≈ ( 1 − n 2 π 2 s 2 ) n
当n → ∞ n \to \infty n → ∞ lim n → ∞ ( 1 − 2 π 2 s 2 n ) n ≈ e − 2 π 2 s 2 \lim_{n\to \infty}\left(1-\frac{2\pi^2s^2}{n} \right)^n \approx e^{-2\pi^2s^2} lim n → ∞ ( 1 − n 2 π 2 s 2 ) n ≈ e − 2 π 2 s 2
F ( n ( p ∗ n ) ( n x ) ) = e − 2 π 2 s 2 \mathcal{F}\left(\sqrt{n}(p^{*n})(\sqrt{n}x)\right) = e^{-2\pi^2s^2}
F ( n ( p ∗ n ) ( n x ) ) = e − 2 π 2 s 2
用傅里叶逆变换求出
p n o r m a l = F − 1 ( e − 2 π 2 s 2 ) = 1 2 π e − x 2 2 p_{normal} = \mathcal{F}^{-1}(e^{-2\pi^2s^2}) = \frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}
p n o r m a l = F − 1 ( e − 2 π 2 s 2 ) = 2 π 1 e − 2 x 2
因此得出结论,当n → ∞ n\to \infty n → ∞
p n o r m a l ( x ) = 1 2 π e − x 2 2 p_{normal}(x) = \frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}
p n o r m a l ( x ) = 2 π 1 e − 2 x 2
其中n可以理解为某个独立随机变量连续测量的次数,当测量次数足够多时,其概率的密度函数会符合正态分布。这也就是我们所称的中心极限定理。
二项分布是正态分布的一个特殊情况,正态分布的随机变量是连续的,而二项分布的变量取值只有两项,是离散的。二项分布在我们的日常生活中比较常见。用游戏抽卡来举个例子,取值只有出货或者没出货两个。设n n n n → ∞ n \to \infty n → ∞
我们把我们前面所学习的傅里叶变换称为传统傅里叶变换。按照我们原来的理论,只有函数的积分收敛了,它才能进行傅里叶变换。如此一来,对于常规的sin \sin sin cos \cos cos
傅里叶变换基于积分的收敛
傅里叶逆变换必须可行,否则尽管傅里叶正变换被执行了也毫无意义
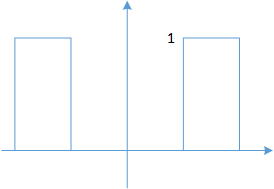
f ( t ) = Π ( t ) f(t) = \Pi(t)
f ( t ) = Π ( t )
F Π = s i n c F Π = ∫ − ∞ ∞ e − 2 π i s t d s F − 1 s i n c = F − 1 F Π = Π F − 1 s i n c = ∫ − ∞ ∞ e 2 π i s t sin π s π s d s F s i n c = F F Π = Π − = Π F s i n c = ∫ − ∞ ∞ e − 2 π i s t sin π s π s d s \begin{aligned}
&\mathcal{F}\Pi = sinc & \mathcal{F}\Pi = \int_{-\infty}^{\infty}e^{-2\pi ist}ds \\
&\mathcal{F}^{-1}sinc = \mathcal{F}^{-1}\mathcal{F}\Pi = \Pi & \mathcal{F}^{-1}sinc = \int_{-\infty}^{\infty}e^{2\pi ist}\frac{\sin\pi s}{\pi s}ds \\
&\mathcal{F}sinc = \mathcal{F}\mathcal{F}\Pi = \Pi^{-} = \Pi & \mathcal{F}sinc = \displaystyle{\int_{-\infty}^{\infty}e^{-2\pi ist}\frac{\sin \pi s}{\pi s}ds }
\end{aligned} F Π = s i n c F − 1 s i n c = F − 1 F Π = Π F s i n c = F F Π = Π − = Π F Π = ∫ − ∞ ∞ e − 2 π i s t d s F − 1 s i n c = ∫ − ∞ ∞ e 2 π i s t π s sin π s d s F s i n c = ∫ − ∞ ∞ e − 2 π i s t π s sin π s d s
在左方的式子中,我们能很轻松地运用傅里叶的逆变换、对偶等定理得到结果,但是在实际应用中我们对信号进行傅里叶转换并处理后,通常需要像右方的式子进行计算后去获得原始的信号,而右方的第二三个式子的积分求法是非常困难的。另外,在计算的时候还必须面对一些函数的收敛性问题——由于Π \Pi Π Π \Pi Π ± 1 2 \pm \frac{1}{2} ± 2 1 1 2 ( 0 + 1 ) \frac{1}{2}(0+1) 2 1 ( 0 + 1 ) Π \Pi Π
f ( t ) = 1 F f ( t ) = ∫ − ∞ ∞ e − 2 π i s t d t f ( t ) = sin 2 π t F f ( t ) = ∫ − ∞ ∞ e − 2 π i s t sin 2 π t d t f ( t ) = cos 2 π t F f ( t ) = ∫ − ∞ ∞ e − 2 π i s t cos 2 π t d t \begin{aligned}
&f(t) = 1 & \mathcal{F}f(t) = \displaystyle{\int_{-\infty}^{\infty}e^{-2\pi ist}dt } \\
&f(t) = \sin2\pi t & \qquad \mathcal{F}f(t) = \displaystyle{\int_{-\infty}^{\infty}e^{-2\pi ist}\sin2\pi t dt } \\
&f(t) = \cos2\pi t & \qquad \mathcal{F}f(t) = \displaystyle{\int_{-\infty}^{\infty}e^{-2\pi ist}\cos2\pi t dt }
\end{aligned} f ( t ) = 1 f ( t ) = sin 2 π t f ( t ) = cos 2 π t F f ( t ) = ∫ − ∞ ∞ e − 2 π i s t d t F f ( t ) = ∫ − ∞ ∞ e − 2 π i s t sin 2 π t d t F f ( t ) = ∫ − ∞ ∞ e − 2 π i s t cos 2 π t d t
对于这些不收敛的函数的积分是无意义的。
有两种方法可以处理这些问题:
针对特殊函数进行特殊的研究
从基础重新研究傅里叶变换,得到一个更鲁棒的、能适用各种函数的新傅里叶变换的定义
在1940年代以前,各种数学家、科学家们都是采用第一种方法,对各种各样的函数进行研究。40年代以后,科学家们开始采用第二种方法,这种方法发展至今已经相当成熟,我们从这里开始研究第二种方法,探究新的傅里叶变换的定义。
首先找出最适合进行傅里叶变换的函数,这类函数被称为S S S S S S
如果f ( t ) ∈ S f(t) \in S f ( t ) ∈ S F f ∈ S \mathcal{F}f \in S F f ∈ S
如果f ( t ) ∈ S f(t) \in S f ( t ) ∈ S f ( t ) f(t) f ( t ) F F − 1 f = f \mathcal{F}\mathcal{F}^{-1}f = f F F − 1 f = f F − 1 F f = f \mathcal{F}^{-1}\mathcal{F}f = f F − 1 F f = f
条件一,排除了Π \Pi Π Π \Pi Π s i n c sinc s i n c s i n c sinc s i n c
条件二,排除了sin , cos \sin,\cos sin , cos
S S S f ( x ) ∈ S f(x) \in S f ( x ) ∈ S
f ( x ) f(x) f ( x ) 对于任何m , n ⩾ 0 m,n \geqslant 0 m , n ⩾ 0 lim x → ± ∞ ∣ x ∣ n ∣ ∂ m ∂ x m f ( x ) ∣ = 0 \displaystyle{ \lim_{x \to \pm \infty} |x|^n\left| \frac{\partial^m}{\partial x^m} f(x)\right| = 0 } x → ± ∞ lim ∣ x ∣ n ∣ ∣ ∣ ∣ ∂ x m ∂ m f ( x ) ∣ ∣ ∣ ∣ = 0
即f ( x ) f(x) f ( x ) 0 0 0 x x x
⇒ \Rightarrow ⇒ 在传统傅里叶变换中我们经常假设∣ f ( x ) ∣ |f(x)| ∣ f ( x ) ∣ ∣ x f ( x ) ∣ |xf(x)| ∣ x f ( x ) ∣
∫ − ∞ ∞ ∣ x f ( x ) ∣ d x < ∞ \displaystyle{\int_{-\infty}^{\infty}|xf(x)|dx < \infty }
∫ − ∞ ∞ ∣ x f ( x ) ∣ d x < ∞
那么x f ( x ) xf(x) x f ( x ) − 2 π i x f ( x ) -2\pi ixf(x) − 2 π i x f ( x )
F ( − 2 π i x f ( x ) ) = ∫ − ∞ ∞ ( − 2 π i x ) e − 2 π i s x f ( x ) d x = ∫ − ∞ ∞ ( ∂ ∂ s e − 2 π i s x ) f ( x ) d x = ∂ ∂ s ∫ − ∞ ∞ e − 2 π i s x f ( x ) d x = ∂ ∂ s ( F f ) ( s ) \begin{aligned}
\mathcal{F}(-2\pi ixf(x))
&= \int_{-\infty}^{\infty}(-2\pi ix)e^{-2\pi isx}f(x)dx \\
&= \int_{-\infty}^{\infty}\left( \frac{\partial}{\partial s}e^{-2\pi isx} \right)f(x)dx \\
&= \frac{\partial}{\partial s}\int_{-\infty}^{\infty}e^{-2\pi isx}f(x)dx \\
&= \frac{\partial}{\partial s}(\mathcal{F}f)(s)
\end{aligned} F ( − 2 π i x f ( x ) ) = ∫ − ∞ ∞ ( − 2 π i x ) e − 2 π i s x f ( x ) d x = ∫ − ∞ ∞ ( ∂ s ∂ e − 2 π i s x ) f ( x ) d x = ∂ s ∂ ∫ − ∞ ∞ e − 2 π i s x f ( x ) d x = ∂ s ∂ ( F f ) ( s )
在∣ x f ( x ) ∣ |xf(x)| ∣ x f ( x ) ∣ F f ( s ) \mathcal{F}f(s) F f ( s ) F ( − 2 π i x f ( x ) ) \mathcal{F}(-2\pi ixf(x)) F ( − 2 π i x f ( x ) ) ∣ x 2 f ( x ) ∣ |x^2f(x)| ∣ x 2 f ( x ) ∣
F ( ( − 2 π i x ) 2 f ( x ) ) = ∫ − ∞ ∞ ( − 2 π i x ) 2 e − 2 π i s x f ( x ) d x = ∫ − ∞ ∞ ( ∂ 2 ∂ 2 s e − 2 π i s x ) f ( x ) d x = ∂ 2 ∂ 2 s ∫ − ∞ ∞ e − 2 π i s x f ( x ) d x = ∂ 2 ∂ 2 s ( F f ) ( s ) \begin{aligned}
\mathcal{F}((-2\pi ix)^2f(x))
&= \int_{-\infty}^{\infty}(-2\pi ix)^2e^{-2\pi isx}f(x)dx \\
&= \int_{-\infty}^{\infty}\left( \frac{\partial^2}{\partial^2 s}e^{-2\pi isx} \right)f(x)dx \\
&= \frac{\partial^2}{\partial^2 s}\int_{-\infty}^{\infty}e^{-2\pi isx}f(x)dx \\
&= \frac{\partial^2}{\partial^2 s}(\mathcal{F}f)(s)
\end{aligned} F ( ( − 2 π i x ) 2 f ( x ) ) = ∫ − ∞ ∞ ( − 2 π i x ) 2 e − 2 π i s x f ( x ) d x = ∫ − ∞ ∞ ( ∂ 2 s ∂ 2 e − 2 π i s x ) f ( x ) d x = ∂ 2 s ∂ 2 ∫ − ∞ ∞ e − 2 π i s x f ( x ) d x = ∂ 2 s ∂ 2 ( F f ) ( s )
以此类推,∣ x n f ( x ) ∣ |x^nf(x)| ∣ x n f ( x ) ∣ F f ( s ) \mathcal{F}f(s) F f ( s ) n n n ∣ x n f ( x ) ∣ |x^nf(x)| ∣ x n f ( x ) ∣ f ( x ) f(x) f ( x ) 1 s n \frac{1}{s^n} s n 1 n n n f ( x ) f(x) f ( x ) F f ( s ) \mathcal{F}f(s) F f ( s ) f ( x ) f(x) f ( x ) F f ( s ) \mathcal{F}f(s) F f ( s )
⇒ \Rightarrow ⇒ 采用与上面的推导过程不同的方法,这里首先假设f ( x ) f(x) f ( x ) f ′ f' f ′ lim x → ± ∞ f ( x ) = 0 \displaystyle{ \lim_{x \to \pm\infty}f(x) = 0 } x → ± ∞ lim f ( x ) = 0
F ( s ) = ∫ − ∞ ∞ e − 2 π i s x f ( x ) d x = [ f ( x ) e − 2 π i s x − 2 π i s ] x = − ∞ x = ∞ − ∫ − ∞ ∞ e − 2 π i s x − 2 π i s f ′ ( x ) d x = 1 2 π i s ∫ − ∞ ∞ e − 2 π i s x f ′ ( x ) d x lim x → ± ∞ f ( x ) = 0 ⇒ [ f ( x ) e − 2 π i s x − 2 π i s ] x = − ∞ x = ∞ = 0 = 1 2 π i s ( F f ′ ) ( s ) \begin{aligned}
\mathcal{F}(s)
&= \int_{-\infty}^{\infty}e^{-2\pi isx}f(x)dx \\
&= \left[ f(x)\frac{e^{-2\pi isx}}{-2\pi is}\right]_{x=-\infty}^{x=\infty} - \int_{-\infty}^{\infty}\frac{e^{-2\pi isx}}{-2\pi is}f'(x)dx \\
&= \frac{1}{2\pi is}\int_{-\infty}^{\infty}e^{-2\pi isx}f'(x)dx \qquad \lim_{x\to\pm\infty}f(x)=0 \Rightarrow \left[ f(x)\frac{e^{-2\pi isx}}{-2\pi is}\right]_{x=-\infty}^{x=\infty}=0 \\
&= \frac{1}{2 \pi is}(\mathcal{F}f')(s)
\end{aligned} F ( s ) = ∫ − ∞ ∞ e − 2 π i s x f ( x ) d x = [ f ( x ) − 2 π i s e − 2 π i s x ] x = − ∞ x = ∞ − ∫ − ∞ ∞ − 2 π i s e − 2 π i s x f ′ ( x ) d x = 2 π i s 1 ∫ − ∞ ∞ e − 2 π i s x f ′ ( x ) d x x → ± ∞ lim f ( x ) = 0 ⇒ [ f ( x ) − 2 π i s e − 2 π i s x ] x = − ∞ x = ∞ = 0 = 2 π i s 1 ( F f ′ ) ( s )
取绝对值,有
∣ F f ( s ) ∣ = ∣ 1 2 π i s ( F f ′ ) ( s ) ∣ = 1 2 π s ∣ ∫ − ∞ ∞ e − 2 π i s x f ′ ( x ) d x ∣ ⩽ 1 2 π s ∫ − ∞ ∞ ∣ e − 2 π i s x ∣ ∣ f ′ ( x ) ∣ d x = 1 2 π s ∫ − ∞ ∞ ∣ f ′ ( x ) ∣ d x = 1 2 π s ∥ f ′ ∥ 1 \begin{aligned}
|\mathcal{F}f(s)|
&= \left|\frac{1}{2\pi is}(\mathcal{F}f')(s)\right| \\
&= \displaystyle{\frac{1}{2 \pi s}\left| \int_{-\infty}^{\infty}e^{-2\pi isx}f'(x)dx\right| }\\
&\leqslant \frac{1}{2\pi s} \int_{-\infty}^{\infty}|e^{-2\pi isx}||f'(x)|dx \\
&= \frac{1}{2\pi s}\int_{-\infty}^{\infty}|f'(x)|dx \\
&= \frac{1}{2\pi s}\left \| f' \right \|_1
\end{aligned} ∣ F f ( s ) ∣ = ∣ ∣ ∣ ∣ 2 π i s 1 ( F f ′ ) ( s ) ∣ ∣ ∣ ∣ = 2 π s 1 ∣ ∣ ∣ ∣ ∫ − ∞ ∞ e − 2 π i s x f ′ ( x ) d x ∣ ∣ ∣ ∣ ⩽ 2 π s 1 ∫ − ∞ ∞ ∣ e − 2 π i s x ∣ ∣ f ′ ( x ) ∣ d x = 2 π s 1 ∫ − ∞ ∞ ∣ f ′ ( x ) ∣ d x = 2 π s 1 ∥ f ′ ∥ 1
∥ f ′ ∥ 1 \left \| f' \right \|_1 ∥ f ′ ∥ 1 f ′ f' f ′ L 1 − n o r m L_1-norm L 1 − n o r m f ′ f' f ′ F f \mathcal{F}f F f 0 0 0 1 s \frac{1}{s} s 1 f ( x ) f(x) f ( x ) f ′ f' f ′ f ′ ′ f'' f ′ ′ lim x → ± ∞ f ( x ) = 0 \displaystyle{ \lim_{x \to \pm\infty}f(x) = 0} x → ± ∞ lim f ( x ) = 0 lim x → ± ∞ f ′ ( x ) = 0 \displaystyle{\lim_{x\to\pm\infty}f'(x)=0 } x → ± ∞ lim f ′ ( x ) = 0
F f ( s ) = ∫ − ∞ ∞ e − 2 π i s x f ( x ) d x = 1 2 π i s ∫ − ∞ ∞ e − 2 π i s x f ′ ( x ) d x ( p i c k i n g u p o n w h e r e w e w e r e b e f o r e ) = 1 2 π i s ( [ f ′ ( x ) e − 2 π i s x − 2 π i s ] x = − ∞ x = ∞ − ∫ − ∞ ∞ e − 2 π i s x − 2 π i s f ′ ′ ( x ) d x ) = 1 ( 2 π i s ) 2 ∫ − ∞ ∞ e − 2 π i s x f ′ ′ ( x ) d x ( lim x → ± ∞ f ′ ( x ) = 0 ⇒ [ f ′ ( x ) e − 2 π i s x − 2 π i s ] x = − ∞ x = ∞ = 0 ) = 1 ( 2 π i s ) 2 ( F f ′ ′ ) ( s ) \begin{aligned}
\mathcal{F}f(s)
&= \int_{-\infty}^{\infty}e^{-2\pi isx}f(x)dx \\
&= \frac{1}{2\pi is}\int_{-\infty}^{\infty}e^{-2\pi isx}f'(x)dx \qquad (picking \ up \ on \ where \ we \ were \ before)\\
&=\frac{1}{2\pi is} \left( \left[f'(x)\frac{e^{-2\pi isx}}{-2\pi is} \right]_{x=-\infty}^{x=\infty} - \int_{-\infty}^{\infty}\frac{e^{-2\pi isx}}{-2\pi is} f''(x)dx\right )\\
&=\frac{1}{(2\pi is)^2}\int_{-\infty}^{\infty}e^{-2\pi isx}f''(x)dx \qquad(\lim_{x\to\pm\infty}f'(x)=0 \Rightarrow \left[f'(x)\frac{e^{-2\pi isx}}{-2\pi is} \right]_{x=-\infty}^{x=\infty}=0)\\
&=\frac{1}{(2\pi is)^2}(\mathcal{F}f'')(s)
\end{aligned} F f ( s ) = ∫ − ∞ ∞ e − 2 π i s x f ( x ) d x = 2 π i s 1 ∫ − ∞ ∞ e − 2 π i s x f ′ ( x ) d x ( p i c k i n g u p o n w h e r e w e w e r e b e f o r e ) = 2 π i s 1 ( [ f ′ ( x ) − 2 π i s e − 2 π i s x ] x = − ∞ x = ∞ − ∫ − ∞ ∞ − 2 π i s e − 2 π i s x f ′ ′ ( x ) d x ) = ( 2 π i s ) 2 1 ∫ − ∞ ∞ e − 2 π i s x f ′ ′ ( x ) d x ( x → ± ∞ lim f ′ ( x ) = 0 ⇒ [ f ′ ( x ) − 2 π i s e − 2 π i s x ] x = − ∞ x = ∞ = 0 ) = ( 2 π i s ) 2 1 ( F f ′ ′ ) ( s )
因此,
∣ F f ( s ) ∣ ⩽ 1 ∣ 2 π s ∣ 2 ∥ f ′ ′ ∥ 1 |\mathcal{F}f(s)| \leqslant \frac{1}{|2\pi s|^2}\left\| f''\right\|_1
∣ F f ( s ) ∣ ⩽ ∣ 2 π s ∣ 2 1 ∥ f ′ ′ ∥ 1
由于f ′ ′ f'' f ′ ′ F f \mathcal{F}f F f 0 0 0 1 s 2 \frac{1}{s^2} s 2 1 f ( x ) f(x) f ( x ) F f ( s ) \mathcal{F}f(s) F f ( s )
把得到的这两个结论结合起来,即f ( x ) f(x) f ( x ) F f ( s ) \mathcal{F}f(s) F f ( s ) f ( x ) f(x) f ( x )
∣ x m ∂ n ∂ x n f ( x ) ∣ ⩽ C m n |x^m\frac{\partial^n}{\partial x^n}f(x)| \leqslant C_{mn}
∣ x m ∂ x n ∂ n f ( x ) ∣ ⩽ C m n
m , n m,n m , n C m n C_{mn} C m n f ( x ) f(x) f ( x ) C m n C_{mn} C m n
∣ x m ∂ n ∂ x n f ( x ) ∣ → 0 a s x → ± ∞ |x^m\frac{\partial^n}{\partial x^n}f(x)| \to 0 \quad as \quad x\to \pm\infty
∣ x m ∂ x n ∂ n f ( x ) ∣ → 0 a s x → ± ∞
在x x x 0 0 0
证明过程如下:
( 2 π i s ) n F f ( s ) = ( F ∂ n ∂ x n f ) ( s ) ∂ n ∂ s n F f ( s ) = F ( ( − 2 π i x ) n f ( x ) ) \begin{aligned}
(2\pi is)^n\mathcal{F}f(s) &= \left( \mathcal{F}\frac{\partial^n}{\partial x^n}f \right )(s) \\
\frac{\partial^n}{\partial s^n}\mathcal{F}f(s) &= \mathcal{F}\left( (-2\pi ix)^n f(x)\right)
\end{aligned} ( 2 π i s ) n F f ( s ) ∂ s n ∂ n F f ( s ) = ( F ∂ x n ∂ n f ) ( s ) = F ( ( − 2 π i x ) n f ( x ) )
把两个等式合并起来
F ( ∂ n ∂ x n ( ( − 2 π i x ) m f ( x ) ) ) = ( 2 π i s ) n ∂ m ∂ s m F f ( s ) ( − 2 π i ) m F ( ∂ n ∂ x n ( x m f ( x ) ) ) = ( 2 π i s ) n ∂ m ∂ s m F f ( s ) ∣ ( − 2 π i ) m ∣ ∣ F ( ∂ n ∂ x n ( x m f ( x ) ) ) ∣ = ∣ ( 2 π i s ) n ∣ ∣ ∂ m ∂ s m F f ( s ) ∣ ( 2 π ) m − n ∣ F ( ∂ n ∂ x n ( x m f ( x ) ) ) ∣ = ∣ s ∣ n ∣ ∂ m ∂ s m F f ( s ) ∣ \begin{aligned} \mathcal{F}\left(\frac{\partial^n}{\partial x^n}((-2\pi ix)^mf(x)) \right ) &=(2\pi is)^n\frac{\partial^m}{\partial s^m}\mathcal{F}f(s) \\
(-2\pi i)^m\mathcal{F}\left(\frac{\partial^n}{\partial x^n}(x^mf(x)) \right ) &= (2\pi is)^n\frac{\partial^m}{\partial s^m}\mathcal{F}f(s) \\
|(-2\pi i)^m|\left| \mathcal{F}\left(\frac{\partial^n}{\partial x^n}(x^mf(x)) \right )\right| &= |(2\pi is)^n|\left|\frac{\partial^m}{\partial s^m}\mathcal{F}f(s)\right| \\
(2\pi)^{m-n}\left| \mathcal{F}\left(\frac{\partial^n}{\partial x^n}(x^mf(x)) \right )\right| &= |s|^n
\left|\frac{\partial^m}{\partial s^m}\mathcal{F}f(s)\right|
\end{aligned} F ( ∂ x n ∂ n ( ( − 2 π i x ) m f ( x ) ) ) ( − 2 π i ) m F ( ∂ x n ∂ n ( x m f ( x ) ) ) ∣ ( − 2 π i ) m ∣ ∣ ∣ ∣ ∣ F ( ∂ x n ∂ n ( x m f ( x ) ) ) ∣ ∣ ∣ ∣ ( 2 π ) m − n ∣ ∣ ∣ ∣ F ( ∂ x n ∂ n ( x m f ( x ) ) ) ∣ ∣ ∣ ∣ = ( 2 π i s ) n ∂ s m ∂ m F f ( s ) = ( 2 π i s ) n ∂ s m ∂ m F f ( s ) = ∣ ( 2 π i s ) n ∣ ∣ ∣ ∣ ∣ ∂ s m ∂ m F f ( s ) ∣ ∣ ∣ ∣ = ∣ s ∣ n ∣ ∣ ∣ ∣ ∂ s m ∂ m F f ( s ) ∣ ∣ ∣ ∣
把∣ F ( ∂ n ∂ x n ( x m f ( x ) ) ) ∣ \left| \mathcal{F}\left(\frac{\partial^n}{\partial x^n}(x^mf(x)) \right )\right| ∣ ∣ F ( ∂ x n ∂ n ( x m f ( x ) ) ) ∣ ∣ L 1 − n o r m L_1-norm L 1 − n o r m
∣ s n ∂ m ∂ s m F f ( s ) ∣ ⩽ ( 2 π ) m − n ∥ ∂ n ∂ x n ( x m f ( x ) ) ∥ 1 \left|s^n\frac{\partial^m}{\partial s^m}\mathcal{F}f(s)\right| \leqslant (2\pi)^{m-n}\left\| \frac{\partial^n}{\partial x^n}(x^mf(x)) \right\|_1
∣ ∣ ∣ ∣ s n ∂ s m ∂ m F f ( s ) ∣ ∣ ∣ ∣ ⩽ ( 2 π ) m − n ∥ ∥ ∥ ∥ ∂ x n ∂ n ( x m f ( x ) ) ∥ ∥ ∥ ∥ 1
由于f ( x ) f(x) f ( x ) C m n C_{mn} C m n
∣ s n ∂ m ∂ s m F f ( s ) ∣ ⩽ C m n \left|s^n\frac{\partial^m}{\partial s^m}\mathcal{F}f(s)\right| \leqslant C_{mn}
∣ ∣ ∣ ∣ s n ∂ s m ∂ m F f ( s ) ∣ ∣ ∣ ∣ ⩽ C m n
因此得结论
F f ( s ) ∈ S a s f ( x ) ∈ S \mathcal{F}f(s) \in S \quad as \quad f(x) \in S
F f ( s ) ∈ S a s f ( x ) ∈ S
逆傅里叶变换与正傅里叶变换只在e e e − - −
F − 1 f ( x ) ∈ S a s f ( s ) ∈ S \mathcal{F}^{-1}f(x) \in S \quad as \quad f(s) \in S
F − 1 f ( x ) ∈ S a s f ( s ) ∈ S
∫ − ∞ ∞ ∣ F f ( s ) ∣ 2 d s = ∫ − ∞ ∞ ∣ f ( x ) ∣ 2 d x \displaystyle{\int_{-\infty}^{\infty}|\mathcal{F}f(s)|^2ds = \int_{-\infty}^{\infty}|f(x)|^2dx }
∫ − ∞ ∞ ∣ F f ( s ) ∣ 2 d s = ∫ − ∞ ∞ ∣ f ( x ) ∣ 2 d x
该等式表明信号在时域与频域的能量相等。其一般形式为:f ( x ) , g ( x ) ∈ S f(x),g(x) \in S f ( x ) , g ( x ) ∈ S
∫ − ∞ ∞ F f ( s ) F g ( s ) ˉ 2 d s = ∫ − ∞ ∞ f ( x ) g ( x ) ˉ d x \displaystyle{\int_{-\infty}^{\infty}\mathcal{F}f(s)\bar{\mathcal{F}g(s)}2ds = \int_{-\infty}^{\infty}f(x)\bar{g(x)}dx }
∫ − ∞ ∞ F f ( s ) F g ( s ) ˉ 2 d s = ∫ − ∞ ∞ f ( x ) g ( x ) ˉ d x
推导过程如下:
g ( x ) = ∫ − ∞ ∞ e 2 π i s x F g ( s ) d s g(x) = \displaystyle{\int_{-\infty}^{\infty}e^{2\pi isx}\mathcal{F}g(s)ds }
g ( x ) = ∫ − ∞ ∞ e 2 π i s x F g ( s ) d s
→ g ( x ) ˉ = ∫ − ∞ ∞ e − 2 π i s x F g ( s ) ˉ d s \rightarrow \quad \bar{g(x)} = \displaystyle{\int_{-\infty}^{\infty}e^{-2\pi isx}\bar{\mathcal{F}g(s)}ds}
→ g ( x ) ˉ = ∫ − ∞ ∞ e − 2 π i s x F g ( s ) ˉ d s
则,
∫ − ∞ ∞ f ( x ) g ( x ) ˉ d x = ∫ − ∞ ∞ f ( x ) ( ∫ − ∞ ∞ e − 2 π i s x F g ( s ) d s ˉ ) d x = ∫ − ∞ ∞ ( ∫ − ∞ ∞ f ( x ) e − 2 π i s x d x ) F g ( s ) ˉ d s = ∫ − ∞ ∞ F f ( s ) F g ( s ) ˉ d s \begin{aligned}
\int_{-\infty}^{\infty}f(x)\bar{g(x)}dx
&= \int_{-\infty}^{\infty}f(x)\left( \int_{-\infty}^{\infty}e^{-2\pi isx}\bar{\mathcal{F}g(s)ds}\right)dx \\
&= \int_{-\infty}^{\infty}\left( \int_{-\infty}^{\infty}f(x)e^{-2\pi isx}dx \right )\bar{\mathcal{F}g(s)}ds \\
&= \int_{-\infty}^{\infty}\mathcal{F}f(s)\bar{\mathcal{F}g(s)}ds
\end{aligned} ∫ − ∞ ∞ f ( x ) g ( x ) ˉ d x = ∫ − ∞ ∞ f ( x ) ( ∫ − ∞ ∞ e − 2 π i s x F g ( s ) d s ˉ ) d x = ∫ − ∞ ∞ ( ∫ − ∞ ∞ f ( x ) e − 2 π i s x d x ) F g ( s ) ˉ d s = ∫ − ∞ ∞ F f ( s ) F g ( s ) ˉ d s
同理,由于∣ e 2 π i s x ∣ = 1 |e^{2\pi isx}| = 1 ∣ e 2 π i s x ∣ = 1
∫ − ∞ ∞ ∣ F f ( s ) ∣ 2 d s = ∫ − ∞ ∞ ∣ f ( x ) ∣ 2 d x \displaystyle{\int_{-\infty}^{\infty}|\mathcal{F}f(s)|^2 ds = \int_{-\infty}^{\infty}|f(x)|^2 dx }
∫ − ∞ ∞ ∣ F f ( s ) ∣ 2 d s = ∫ − ∞ ∞ ∣ f ( x ) ∣ 2 d x
速降函数φ ( x ) \varphi (x) φ ( x )
φ ( x ) \varphi(x) φ ( x ) 对于任意m , n m,n m , n
∣ x ∣ n ∣ ∂ m ∂ x m φ ( x ) ∣ → 0 a s x → ± ∞ |x|^n\left| \frac{\partial ^m}{\partial x^m}\varphi(x) \right| \to 0 \quad as \quad x\to \pm\infty
∣ x ∣ n ∣ ∣ ∣ ∣ ∂ x m ∂ m φ ( x ) ∣ ∣ ∣ ∣ → 0 a s x → ± ∞
为什么速降函数是傅里叶变换的最佳函数呢?
如果φ ( x ) ∈ S \varphi(x)\in S φ ( x ) ∈ S F φ ( s ) ∈ S \mathcal{F}\varphi(s) \in S F φ ( s ) ∈ S
φ ∈ S ⇒ F − 1 F φ = φ , F F − 1 φ = φ \varphi \in S \quad \Rightarrow \quad \mathcal{F}^{-1}\mathcal{F}\varphi=\varphi \ ,\ \mathcal{F}\mathcal{F}^{-1}\varphi = \varphi φ ∈ S ⇒ F − 1 F φ = φ , F F − 1 φ = φ
Π ∉ S \Pi \notin S Π ∈ / S Λ ∉ S \Lambda \notin S Λ ∈ / S cos \cos cos s i n sin s i n ∉ S \notin S ∈ / S S S S
这里的分布不同于概率上的分布,它是广义上的函数(generalized function)的名称。
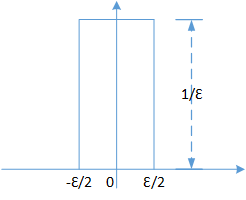
δ \delta δ δ \delta δ δ \delta δ δ \delta δ Π \Pi Π δ \delta δ
δ = lim ε → 0 1 ε Π ε ( x ) \delta = \displaystyle{\lim_{\varepsilon\to 0}\frac{1}{\varepsilon}\Pi_{\varepsilon}(x) }
δ = ε → 0 lim ε 1 Π ε ( x )
对δ \delta δ
∫ − ∞ ∞ 1 ε Π ε ( x ) d x = 1 ε ∫ − ε 2 ε 2 1 d x = 1 , ε → 0 \int_{-\infty}^{\infty}\frac{1}{\varepsilon}\Pi_{\varepsilon}(x)dx= \frac{1}{\varepsilon}\int_{-\frac{\varepsilon}{2}}^{\frac{\varepsilon}{2}}1dx = 1 \qquad, \varepsilon \to 0
∫ − ∞ ∞ ε 1 Π ε ( x ) d x = ε 1 ∫ − 2 ε 2 ε 1 d x = 1 , ε → 0
δ \delta δ φ ( x ) \varphi(x) φ ( x )
∫ − ∞ ∞ 1 ε Π ε ( x ) φ ( x ) d x = 1 ε ∫ − ε 2 ε 2 φ ( x ) d x = 1 ε ∫ − ε 2 ε 2 ( φ ( 0 ) + φ ′ ( 0 ) x + 1 2 φ ′ ′ ( 0 ) x 2 + . . . ) d x ( T a y l o r s e r i e s ) = φ ( 0 ) + 0 ( ε ) ( a s ε → 0 , t e r m s a f t e r φ ( 0 ) t u r n t o 0 ) = φ ( 0 ) \begin{aligned}
\int_{-\infty}^{\infty}\frac{1}{\varepsilon}\Pi_{\varepsilon}(x)\varphi(x)dx
&= \frac{1}{\varepsilon}\int_{-\frac{\varepsilon}{2}}^{\frac{\varepsilon}{2}}\varphi(x)dx \\
&= \frac{1}{\varepsilon}\int_{-\frac{\varepsilon}{2}}^{\frac{\varepsilon}{2}}\left(\varphi(0)+\varphi'(0)x+\frac{1}{2}\varphi''(0)x^2+... \right )dx \qquad (Taylor \ series)\\
&= \varphi(0)+0(\varepsilon) \qquad (as\ \varepsilon\to 0, terms \ after \ \varphi(0) \ turn \ to \ 0 )\\
&= \varphi(0)
\end{aligned} ∫ − ∞ ∞ ε 1 Π ε ( x ) φ ( x ) d x = ε 1 ∫ − 2 ε 2 ε φ ( x ) d x = ε 1 ∫ − 2 ε 2 ε ( φ ( 0 ) + φ ′ ( 0 ) x + 2 1 φ ′ ′ ( 0 ) x 2 + . . . ) d x ( T a y l o r s e r i e s ) = φ ( 0 ) + 0 ( ε ) ( a s ε → 0 , t e r m s a f t e r φ ( 0 ) t u r n t o 0 ) = φ ( 0 )
即,
lim ε → 0 ∫ − ∞ ∞ 1 ε Π ε ( x ) φ ( x ) d x = φ ( 0 ) \displaystyle{\lim_{\varepsilon\to 0}\int_{-\infty}^{\infty}\frac{1}{\varepsilon}\Pi_{\varepsilon}(x)\varphi(x)dx = \varphi(0) }
ε → 0 lim ∫ − ∞ ∞ ε 1 Π ε ( x ) φ ( x ) d x = φ ( 0 )
如果是单单观察δ \delta δ δ \delta δ f ( x ) f(x) f ( x ) 0 0 0 δ \delta δ
测试函数φ \varphi φ
跟这些测试函数相关的,我们称之为广义函数或者分布。一个分布T T T T ( φ ) T(\varphi) T ( φ ) T T T φ \varphi φ T ( φ 1 + φ 2 ) = T ( φ 1 ) + T ( φ 2 ) , T ( a φ ) = a T ( φ ) T(\varphi_1+\varphi_2) = T(\varphi_1)+T(\varphi_2) \quad , \quad T(a\varphi) = aT(\varphi) T ( φ 1 + φ 2 ) = T ( φ 1 ) + T ( φ 2 ) , T ( a φ ) = a T ( φ )
如果φ n \varphi_n φ n φ \varphi φ T T T φ n \varphi_n φ n T T T φ \varphi φ
φ n → φ ⇒ T ( φ n ) → T ( φ ) \varphi_n\to \varphi \quad \Rightarrow \quad T(\varphi_n)\to T(\varphi)
φ n → φ ⇒ T ( φ n ) → T ( φ )
f u n c t i o n s f u n c t i o n n u m b e r s n u m b e r functions \ function \ numbers \ number
f u n c t i o n s f u n c t i o n n u m b e r s n u m b e r
分布作用于φ \varphi φ < T , φ > < T , φ > T ( φ ) T(\varphi) T ( φ ) < T , φ > < T , φ >
δ \delta δ δ \delta δ δ \delta δ φ \varphi φ δ \delta δ φ \varphi φ
< δ , φ > = φ ( 0 ) <\delta,\varphi> = \varphi(0)
< δ , φ > = φ ( 0 )
线性:
< δ , φ 1 + φ 2 > = ( φ 1 + φ 2 ) ( 0 ) = φ 1 ( 0 ) + φ 2 ( 0 ) = < δ , φ 1 > + < δ , φ 2 > <\delta,\varphi_1+\varphi_2> = (\varphi_1+\varphi_2)(0) = \varphi_1(0)+\varphi_2(0) = <\delta,\varphi_1>+<\delta,\varphi_2>
< δ , φ 1 + φ 2 > = ( φ 1 + φ 2 ) ( 0 ) = φ 1 ( 0 ) + φ 2 ( 0 ) = < δ , φ 1 > + < δ , φ 2 >
收敛性:
< δ , φ n > = φ n ( 0 ) <\delta,\varphi_n> = \varphi_n(0)
< δ , φ n > = φ n ( 0 )
< δ , φ > = φ ( 0 ) <\delta,\varphi> = \varphi(0)
< δ , φ > = φ ( 0 )
函数序列φ n \varphi_n φ n φ \varphi φ φ n ( 0 ) \varphi_n(0) φ n ( 0 ) φ ( 0 ) \varphi(0) φ ( 0 )
φ n → φ ⇒ φ n ( 0 ) → φ ( 0 ) ⇒ < δ , φ n > → < δ , φ > \varphi_n\to \varphi \quad \Rightarrow \quad \varphi_n(0)\to \varphi(0) \quad \Rightarrow \quad <\delta, \varphi_n>\to <\delta,\varphi>
φ n → φ ⇒ φ n ( 0 ) → φ ( 0 ) ⇒ < δ , φ n > → < δ , φ >
δ \delta δ ∫ − ∞ ∞ δ ( x − y ) f ( y ) d y = f ( x ) \displaystyle{\int_{-\infty}^{\infty}\delta(x-y)f(y)dy = f(x) }
∫ − ∞ ∞ δ ( x − y ) f ( y ) d y = f ( x )
该式子表明了δ \delta δ x x x f f f f ( x ) f(x) f ( x ) x = 0 x=0 x = 0 δ a \delta_a δ a
< δ a , φ > = φ ( a ) <\delta_a,\varphi> = \varphi(a)
< δ a , φ > = φ ( a )
我们在讨论速降函数的时候排除了Π , Λ , sin , cos \Pi,\Lambda,\sin,\cos Π , Λ , sin , cos f ( x ) = 1 f(x) = 1 f ( x ) = 1 1 1 1 φ \varphi φ
< 1 , φ > = ∫ − ∞ ∞ 1 φ ( x ) d x <1,\varphi> = \displaystyle{\int_{-\infty}^{\infty}1\varphi(x)dx }
< 1 , φ > = ∫ − ∞ ∞ 1 φ ( x ) d x
同理
< Π , φ > = ∫ − ∞ ∞ Π ( x ) φ ( x ) d x <\Pi,\varphi> = \displaystyle{\int_{-\infty}^{\infty}\Pi(x)\varphi(x)dx}
< Π , φ > = ∫ − ∞ ∞ Π ( x ) φ ( x ) d x
< sin 2 π x , φ > = ∫ − ∞ ∞ sin 2 π x φ ( x ) d x <\sin2\pi x,\varphi> = \displaystyle{\int_{-\infty}^{\infty}\sin2\pi x\varphi(x)dx }
< sin 2 π x , φ > = ∫ − ∞ ∞ sin 2 π x φ ( x ) d x
匹配的运算过程,就是通过对T T T φ \varphi φ
< T , φ > = ∫ − ∞ ∞ T ( x ) φ ( x ) d x = \displaystyle{\int_{-\infty}^{\infty}T(x)\varphi(x)dx }
< T , φ > = ∫ − ∞ ∞ T ( x ) φ ( x ) d x
并非所有函数都会在匹配后积分收敛,但是大多数的函数,甚至特别奇异的函数都能使得积分收敛,匹配成立,因为测试函数是很优秀的。对于傅里叶变换来说,速降函数作为测试函数就足够优秀,在这种情况下Π , Λ , sin , cos \Pi,\Lambda,\sin,\cos Π , Λ , sin , cos